¶ 1 DWA
第一章详细解释 DWA 实现方式;第二、三章深入解释 DWA 导致的 Tone;第四章介绍了 Tone Transfer & Suppression 技术 ;第五章列出了参考文献
¶ 1.1 轮巡规则
DWA 技术最早的提出是如下这篇论文
R. T. Baird and T. S. Fiez, “Linearity enhancement of multibit ΣΔ A/D and D/A converters using data weighted averaging,” IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 42, no. 12, pp. 753–762, Dec. 1995.
DWA 技术很好,基本含义就是就是轮巡着使用,举一个 8 Element (E1 ~ E8) 的例子,可以看使用 DWA 技术反馈5次后,每个 Element 使用的次数都是相等的。数学上实现了对 Mismatch Noise 的一阶整形
| 反馈次序 | 反馈的数值 | 正常使用的 Element | DWA使用的 Element |
|---|---|---|---|
| 1 | 2 | E1 E2 | E1 E2 |
| 2 | 4 | E1 E2 E3 E4 | E3 E4 E5 E6 |
| 3 | 3 | E1 E2 E3 | E7 E8 E1 |
| 4 | 5 | E1 E2 E3 E4 E5 | E2 E3 E4 E5 E6 |
| 5 | 2 | E1 E2 | E7 E8 |
¶ 1.2 编码规则
通常我们的 DAC 都是基于 element 叠加使用的,比如 CDAC 和 IDAC, element 的个数就是 Full-Scale Range,对于一个 8 Element 的 DAC,E1=E2=E3=E4... 到 2-Level Element 映射关系如下,2-Level Element 分为 Unipolar (+1/0) 和 Bipolar (+1/-1) 两种
| 温度计码 | 反馈+1的Element | 反馈0或者-1的Element | Unipolar (+1/ 0) | Bipolar (+1/ -1) |
|---|---|---|---|---|
| 0 | E1+E2+E3+E4+E5+E6+E7+E8 | +0 | -8 | |
| 1 | E1 | E1+E2+E3+E4+E5+E6+E7 | +1 | -6 |
| 2 | E1+E2 | E1+E2+E3+E4+E5+E6 | +2 | -4 |
| 3 | E1+E2+E3 | E1+E2+E3+E4+E5 | +3 | -2 |
| 4 | E1+E2+E3+E4 | E1+E2+E3+E4 | +4 | 0 |
| 5 | E1+E2+E3+E4+E5 | E1+E2+E3 | +5 | +2 |
| 6 | E1+E2+E3+E4+E5+E6 | E1+E2 | +6 | +4 |
| 7 | E1+E2+E3+E4+E5+E6+E7 | E1 | +7 | +6 |
| 8 | E1+E2+E3+E4+E5+E6+E7+E8 | +8 | +8 |
¶ 1.3 电路结构
DWA的实现方式,通常包含如下组件
Pointer Accumulator
DWA 的核心是“循环使用”DAC 单元。指针维护模块负责“记住”上一次使用到了哪个 DAC 单元。它是一个模加法器(Modulo Adder)。如果 ADC 的量化级数为 ,当前输入数据为 ,上一时刻的指针为 ,则当前指针计算公式为:
| [n] | Din | PTR | Used Element | Notation |
|---|---|---|---|---|
| 0 | - | 0 | - | 初始状态 |
| 1 | 2 | 0+2 = 2 | E1 E2 | 移动 PTR[n-1]=0 |
| 2 | 4 | 2+4=6 | E3 E4 E5 E6 | 移动 PTR[n-1]=2 |
| 3 | 3 | (6+3) mod 8 =1 | E7 E8 E1 | 移动 PTR[n-1]=6 |
| 4 | 5 | 1+5=6 | E2 E3 E4 E5 E6 | 移动 PTR[n-1]=1 |
| 5 | 2 | E1 E2 | E7 E8 | 移动 PTR[n-1]=6 |
典型结构是由一个 加法器 (Adder) 和一个 寄存器 (Register) 组成。在高速 Sigma-Delta ADC 中,这个加法器的进位链(Carry chain)往往是速度瓶颈之一
Bin2Therm (Binary-to-Thermometer Converter)
DWA 的输入通常是二进制码,而 DAC 阵列需要温度计码控制。此模块将二进制数值 转换为“有 个 1”的温度计码,它是 Barrel Shuffler 的前级,生成原始的、未移位的开启图案(例如 0000111),虽然 Quantizer 生成的就是这个 Thermometer Code,但是原始的 Thermometer Code 并不能直接使用,但是通常需要处理掉 Bubble 才能去使用。
Therm2Bin (Thermometer-to-Binary Converter)
将 Flash Quantizer 输出的温度计码(处理过 Bubble)压缩为二进制码,用于送给 Pointer Accumulator 中的加法器使用
Barrel Shuffler (筒形移位洗牌器)
Barrel Shuffler 的作用是根据 指针 (PTR) 的值,将 Bin2Therm 生成的原始温度计码进行循环左移 (Circular Left Shift),DWA 需要的是循环移位,即 Rotate,而非单纯的 Shift。关于 Barrel Shuffler(以及更广泛的 DWA 硬件实现结构)的演进,确实有一条清晰的脉络:从最早的直接映射(Matrix),到标准化的对数结构(Logarithmic),再到为了应对超高速(GHz)而诞生的“分段/树形”或“预测型”结构。详见 Barrier-Shuffler
¶ 2 DWA 行为观察 (TI)
TI 的这篇文献,没有复杂的数学推导,但是结合仿真给出了一些直观分析,对理解 Tone 的行为很有帮助
F. Chen and B. Leung, “Some observations on tone behavior in data weighted averaging,” in Proc. IEEE ISCAS, May 1998, pp. 500–503.
¶ 2.1 Input Amplitude
对于 Amplitude,0 输入附近,在 Bipolar 反馈中,就是用一半的 Element,因此 Tone 就在 fs/2 附近;随着输入 Amplitude 提高,轮巡的速度变慢,也就越来越往低频走了;
¶ 2.2 Integrator DC Gain
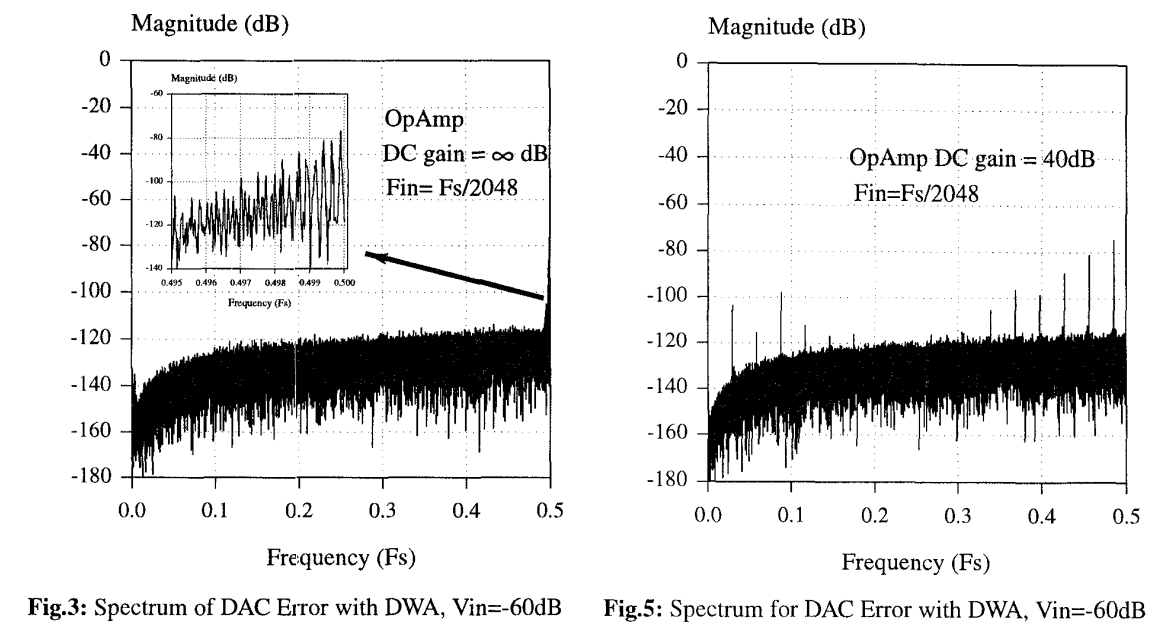
为了达到期望的分辨率, 调制器需要提供足够的环路增益(在带宽内)以衰减基带内的量化噪声 。经验法则是运放直流增益不应低于过采样率 。然而,上述经验法则并不适用,因为在使用 DWA 时,相对较低的运放直流增益 (≤50dB) 会产生大的单音 。由于运放直流增益决定了调制器的直流衰减,输出模式会被直流增益改变 。如前所述,正是这种周期性模式与 DAC 误差相互作用产生了单音 。图 5 显示了输入电平为 -60dB、直流增益为 40dB 时的典型 DAC 误差频谱 。与图 3 相比,原本在低频的单音在幅度和频率上都增加了并向上传播,而高频的单音则向下传播 。观察结果是,增加运放直流增益将使单音分别在低频和高频范围内聚集,并最终将这两个簇分别推向更远的 DC 和 。因此,当使用 DWA 时,对运放直流增益的要求并不像使用其他算法那样宽松 。在实际设计中,运放直流增益应该进行过设计(Over-designed)
¶ 2.3 OSR Sampling Frequency
对于高速应用,可能会使用极低的过采样率(例如 )。在如此低的 OSR 下,必须考虑混叠效应。对于总数为 M 的 DAC 元件 (),使用 DWA 时最低的单音频率可能位于 。最高频率 () 的大基波及其谐波失真 (HD) 分量 () 随后会被此单音调制。因此,为了不让谐波失真落入基带,必须满足以下不等式: 。
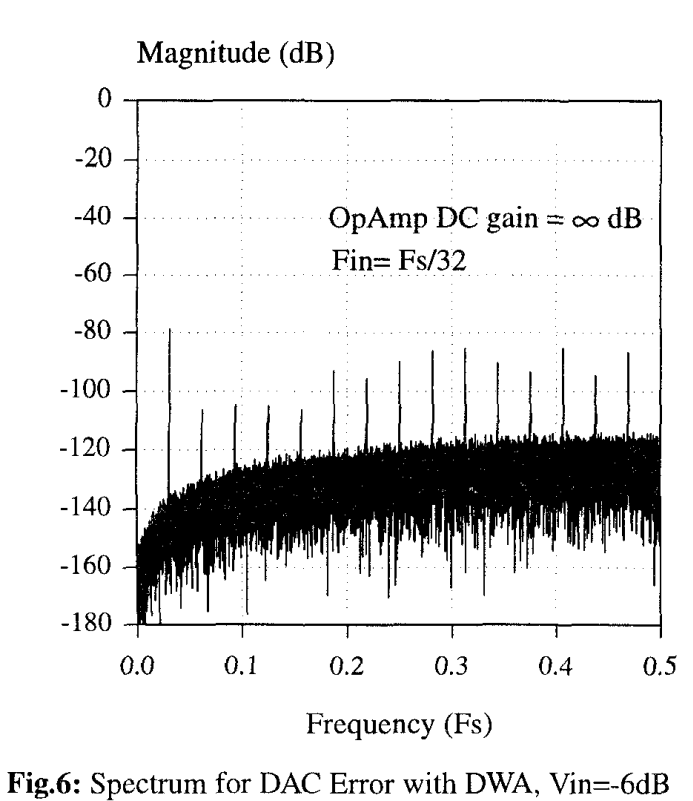
于是我们可以推导出避免混叠的条件为: 。例如,如果 且 ,则 OSR 必须大于 64;或者如果 ,M 不能大于 4。图 6 显示, 处的测试基波信号的谐波回混到了整个频带,直至 。可以预期,当模拟输入幅度较小时,这些混叠单音(更准确地说是谐波失真)将会消失 。DWA 的这种混叠问题最终可能会对在低 OSR 的 调制器中使用 DWA 施加严重的限制 。
这里的 n 指的是基波的谐波失真,举得例子是3,或许我们可以理解为,更高阶的谐波只有很低的能量,我们管好 3 阶以内的就好了
¶ 3 深刻理解 DWA Tone
¶ 3.1 固定 DAC INPUT 下的 Tone
为了简化分析,我们以 Unipolar=8,DAC 的反馈能力是 0:1:8,如果每次 DAC 要反馈的值总是 4 的话会发生什么
- 假设输入的 DC 值是 4,那么每进行 2 次采样就会完成一次 Element 从 0 开始到 8 恰好结束,那么这会造成一个 fs/2 的 Tone;
- 假设输入的 DC 值是 2,那么每进行 4 次采样就会完成一次 Element 从 0 开始到 8 恰好结束,那么这会造成一个 fs/4 的 Tone;
- 假设输入的 DC 值是 3,那么每进行 8 次采样就会完成一次 Element 从 0 开始到 8 恰好结束,那么这会造成一个 fs/8 的 Tone;
- 假设输入的 DC 值是 1/2,那么每进行 16 次采样就会完成一次 Element 从 0 开始到 8 恰好结束,那么这会造成一个 fs/16 的 Tone;
这样我们得出一个结论,DAC 产生的 Tone 的频率是
假设输入的 DC 值是 3/4,3/4 和 8 的最大公约数 1/4,按照公式计算产生 Tone 的频率是 fs/32;观察32,每进行32次采样,32×(3/4) = 8×3,确实每进行 32 次采样就能让 Element 的使用从 0 开始且恰好结束于 8
¶ 3.2 Amplitude
这部分内容来自 K. D. Chen and T. H. Kuo, “An improved technique for reducing baseband tones in sigma–delta modulators employing data weighted averaging algorithm without adding dither,” IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 46, no. 1, pp. 63–68, Jan. 1999.
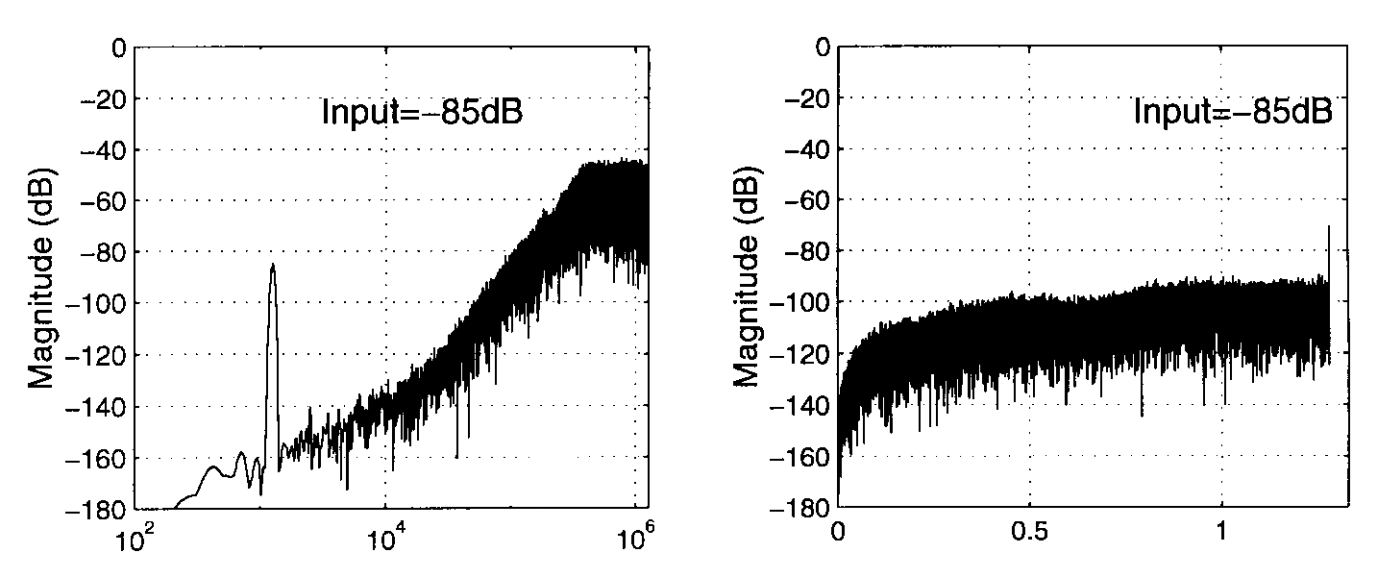
Amplitude =-85dB
- 当具有奇数个量化电平时, 9-Level-Biploar-8Element,我们总是会大量的反馈4,伴随少量的3和5;这个 4 就意味着没进行2次反馈,就完成了一次 DWA 的轮巡,实现的平均误差 (DC误差) 为0,主要会看到一个 fs/2 的 Tone
- 当具有奇数个量化电平时,8-Level-Biploar-7Element,我们总是会大量平等地反馈 3 和 4,可能伴随少量的 2 和 5;这个 3 和 4 恰好构成 7 个 element 的周期,也和奇数个量化电平的效果一样,每2次反馈线性平均误差为0,这样会看到一个 fs/2 的 Tone
如下图,是一个 -80dB输入下,Quantizer Output(左图),DAC Error Output(右图)
Amplitude =-45dB
接着我们继续分析奇数个量化电平的情况,9-Level-Biploar-8Element,随着输入信号增大,原先少量的 3 和 5 的概率增加了,这在相位的上面,一直反馈 4 是一个理想的 fs/2 的频率,反馈 3 代表着相位滞后,反馈 5 代表着相位超前,相位噪声在频谱上就表现除了裙带,着就意味着 fs/2 这里本来集中的频谱,开始变胖了
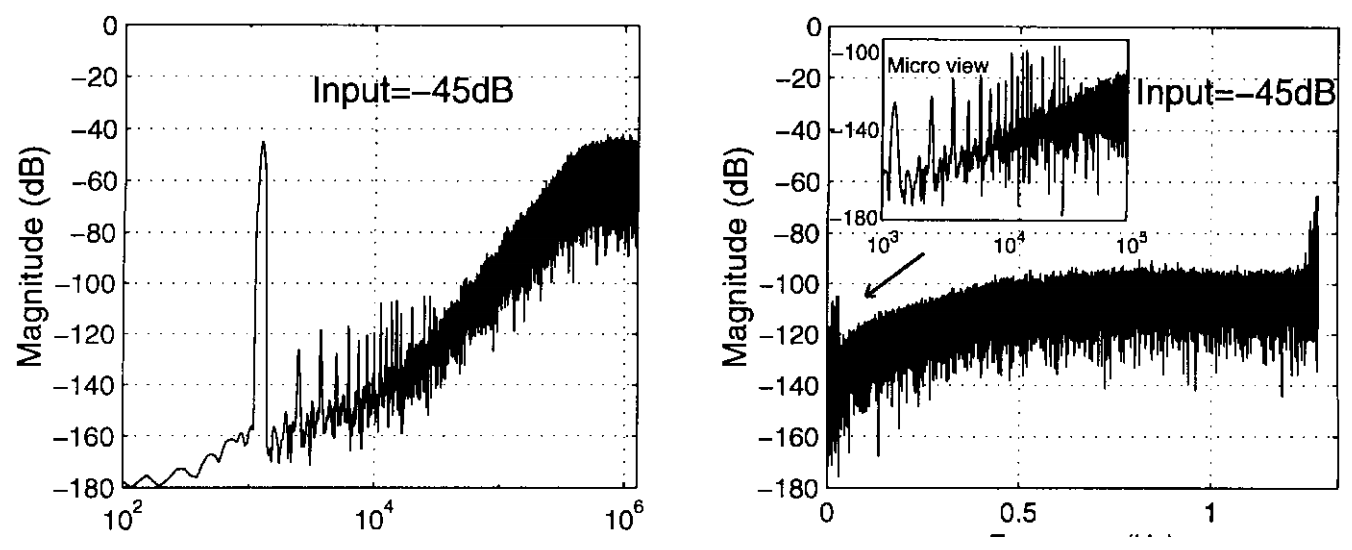
如果 3 和 5 是完全随机出现的(像抛硬币一样),那么这种扩散是白噪声,可能还好。 但问题是,3 和 5 的出现是由量化噪声(Quantizer Noise)控制的,Quantizer Noise 并不是完全随机的
- 量化器的逻辑:我现在误差积累太大了(正向),我需要输出一个 5 来快速修正
- DWA 的反应:好,既然你输出了 5,我的指针就多跳一格。
- DAC 元件的运气:这就导致,每次量化器想要“修正正向误差”的时候,DWA 指针总是倾向于跳到某些特定的元件上。
虽然 3 和 5 是等概率出现的,但是并不是 3 和 5 的概率相等就能抵消。 抵消的前提是误差必须也是等概率地落在 3 和 5 的时刻上。
Amplitude =-4dB
当输入接近满量程的时候,一个接近满量程的正选信号,能让 DAC Code 尽可能均匀的使用,因此也不会出现明显的 DAC Mismatch Error Tone,甚至连 fs/2 那个基频都没有了,因为实在是太“普渡众生”了
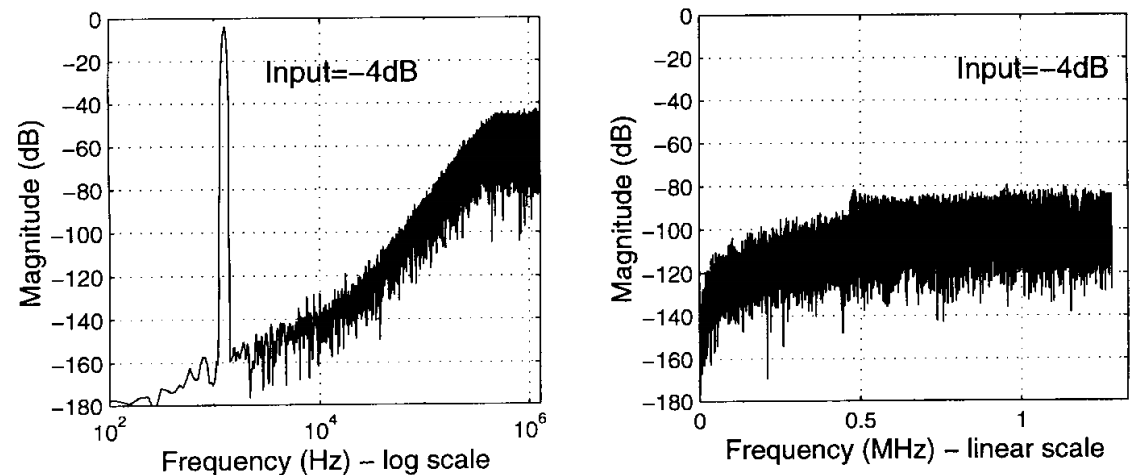
¶ 3.3 顿悟 DWA 机制
从频率上理解 Amplitude =-45dB,涉及到 PM 相位调制,AM调制能够实现载波抑制,调完之后载波频率 就没有了,值剩下了
而 DWA 被 Quantizer Noise 改变的,其实是相位调制
- :这是由 Code 4 决定的平均旋转频率。
- :这是由 Code 3(慢)和 Code 5(快)引起的相位偏差。因为 3/5 是由量化噪声驱动的,所以 的频谱成分对应量化噪声( 附近的一坨)。
利用三角公式展开这个 PM 信号
当相位抖动 比较小的时候, 意味着载波存活,并发生了一些扩展;第二部分, , 主要是频率在 附近的量化噪声, 的频率是 ,这就发生了如 AM 调制一半的频率搬移,差频和和频分别在 和 ,也就是 DC 附近的频率
更深刻的理解是: ,也就是 Quantizer Ouput,如果不存在 limit cycle,能量的分散开的不集中,那 决定的 PM调制 的第二项,类似 AM 调制,调制完的 DAC Mismatch Noise 就是是平滑的,没有突兀的 Tone,也就是说 dither 也可以解决 DWA 中 DC 输入下的这个 tone 的问题。所以 quantizer limit Cycle 导致的,不仅仅是 Quantizer 的 tone,还有 DAC Mismatich 的 tone
¶ 4 DWA 改良
Advancing Data Weighted Averaging Technique for Multi-Bit Sigma–Delta Modulators,这篇论文的综述体现作者的功力,将解决 DWA Tone 的思路分成了以下几大类
- 音调抑制技术(Tone-Suppressing Techniques):此类技术通过引入随机性或改变规则来“打散”周期性,从而消除明显的尖峰音调,但代价是破坏了理想的一阶整形,导致基带底噪(Noise Floor)升高
- 音调转移技术(Tone-Transferring Techniques):此类技术试图保留 DWA 的一阶整形特性(低底噪),通过确定性的规则将音调移到更高的频率(带外)。其主要弱点是对 DC 输入敏感,因为 DC 输入非常容易让其陷入固有周期中去。
¶ 4.1 Advanced DWA
在 #3.1 固定 DAC INPUT 下的 Tone 这里的分析中,其实有一个潜台词,我越快地转完整个周期,那 Tone 就越会往 Fs/2 去聚集
Advancing Data Weighted Averaging Technique for Multi-Bit Sigma–Delta Modulators, 2007
这篇论文中,就是利用这一点,每当用完一圈 Element 后,我就提前一点,提前量可以选择 1 2 3 等等;理解这个过程可以分以下3中情况:
- 正常轮巡,这个就是 DWA 的模式
- 触发跳过,每次遇到周期起点,我就提前 S 个,同时将周期起点也 + S
- 如果这次用的 Element 很多,我跳过 S 个后,发现用的和头重合了,那就触发保护,依然按照 DWA 的方式进行
下面这是一个 S=1 的实例
| 步骤 | 输入 | 指针 | 使用的 Element | 周期起点 | 备注 |
|---|---|---|---|---|---|
| STEP1 | 4 | 0 | 0 1 2 3 | 0 | 正常轮巡 |
| STEP2 | 5 | 4 | 4 5 6 7 1 | 1 | 触发跳过,周期起点+1 |
| STEP3 | 4 | 2 | 2 3 4 5 | 1 | 正常轮巡 |
| STEP4 | 5 | 6 | 6 7 0 2 3 | 2 | 触发跳过,周期起点+1 |
| STEP5 | 5 | 4 | 4 5 6 7 0 | 2 | 正常轮巡 |
| STEP6 | 8 | 1 | 1 2 3 4 5 6 7 0 | 2 | 触发保护,因为如果把2跳过,就会重复使用1 |
| STEP7 | 7 | 1 | 1 3 4 5 6 7 0 | 3 | 触发跳过,周期起点+1 |
| STEP8 | 4 | 1 | 1 2 4 5 | 4 | 触发跳过,周期起点+1 |
论文额外留了一手,其实每次都跳过 S 个,只是将轮巡频率变快,让 Tone 的频率提高而已,在低 OSR 情况下,还是可能会落回到 BASEBAND 中去,因此提出,每次触发跳过,可以让 S=1 或者 S=2,至于到底是 S=1 还是 S=2,则用一个随机序列去控制,这样可以打破周期性。但是这会导致 BASEBAND 的底噪提高,这和所有 Randomized DWA 技术的问题是一样的
¶ 4.2 Bi-Directional DWA
这个解决 DWA 的方法,简单粗暴有效,就是在反馈奇数 DAC 时右旋,反馈偶数 DAC 时左旋,这样在低 OSR 下带内也不会看到明显的 Tone。
虽然原文作者说他保留了 DWA 一阶整形的部分效果,原文作者也通过仿真看到了底噪提高了。在我看来,其实这就是 Randomized DWA,因为由于 Quantizer Noise 可以近似理解为白噪声,在其 Target 值附近的扰动导致的奇偶性,不就是 random signal 嘛
ISSCC文章短小精干,没有废话,这里对其核心思想做些评论
I. Fujimori, L. Longo, A. Hairapetian, K. Seiyama, S. Kosic, J. Cao, and S. L. Chan, “A 90-dB SNR 2.5-MHz output-rate ADC using cascaded multibit delta-sigma modulation at 8X oversampling ratio,” IEEE J. Solid-State Circuits, vol. 35, no. 12, pp. 1820–1828, Dec. 2000.
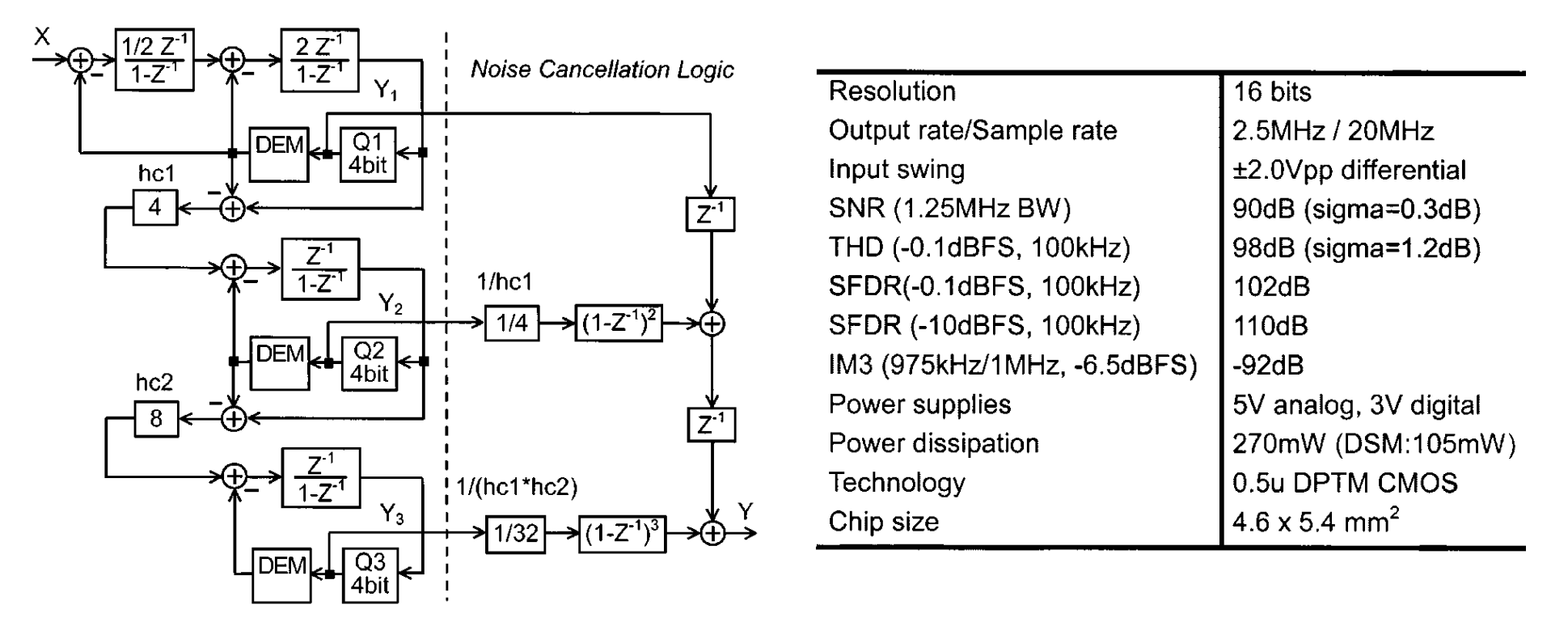
论文的应用场景是用 MASH 2-1-1, OSR=8, ODR=2.5MHz 下实现了 90 dB 的 SNR,这是一个非常高的水平,来自于 Broadcom。整个逻辑链条如下
- 使用 MASH 2-1-1-1 是为了实现高阶 Noise-Shaping 而不带来稳定性问题
- 1bit Quantizer 的 MASH 2-1-1 只有 54 dB,且 MASH 结构依赖于完美抵消,因此需要较高的 OSR 去抑制泄露噪声
- 为了以较低 OSR 去实现,就用了多 Bit 量化器
- 因为后级的输入是前级的 Quantizer Noise,使用多 Bit 量化器降低了后级的输入,为了尽可能用满 Full-Scale,提高信噪比,这里提供了级间增益
- 然后以 Bi-DWA 的方式解决了Multi-Bit Quantizer Mismatch 问题
这篇文论,除了 Bi-DWA,其实其他东西都是我们已知的技术,但是这篇将现有技术优雅高效地工程化落地,值得我们借鉴
¶ 4.3 Incremental DWA
在这篇论文中,最先提出了 Incremental DWA 这个技术
K. D. Chen and T. H. Kuo, “An improved technique for reducing baseband tones in sigma–delta modulators employing data weighted averaging algorithm without adding dither,” IEEE Trans. Circuits Syst. II, Analog Digit. Signal Process., vol. 46, no. 1, pp. 63–68, Jan. 1999.
所谓 Incremental DWA,就是说如果正常使用的 Element 数是 N 的话,我多用 K 个 ELEMENT 去做轮巡,也是非常简单,其背后的机理是,公式如下,GCD = Greatest Common Divisor,最大公约数
这样的效果是,让原本 0 输入下集中在 fs/2 附近的能量(这部分能量在 PM 调制作用下会让 Mismatch Noise 的 Tone 落到 Baseband 内),转移到了的了 fs/(N+K),从而非常低频处的 Tone 问题,详见 #顿悟 DWA 机制
另外值得一提的是,同一个作者,在 2002 年的 JSSC,T. H. Kuo, K. D. Chen, and H. R. Yeng, “A wideband CMOS sigma–delta modulator with incremental data weighted averaging,” IEEE J. Solid-State Circuits, vol. 37, no. 1, pp. 11–17, Jan. 2002. 这篇论文与 Bi-DWA 对比阅读非常有意思,这也是一篇 JSSC,不使用 MASH (大家都这么做)而使用单环路硬做 4th-Order CIFF 的方式实现了如下性能
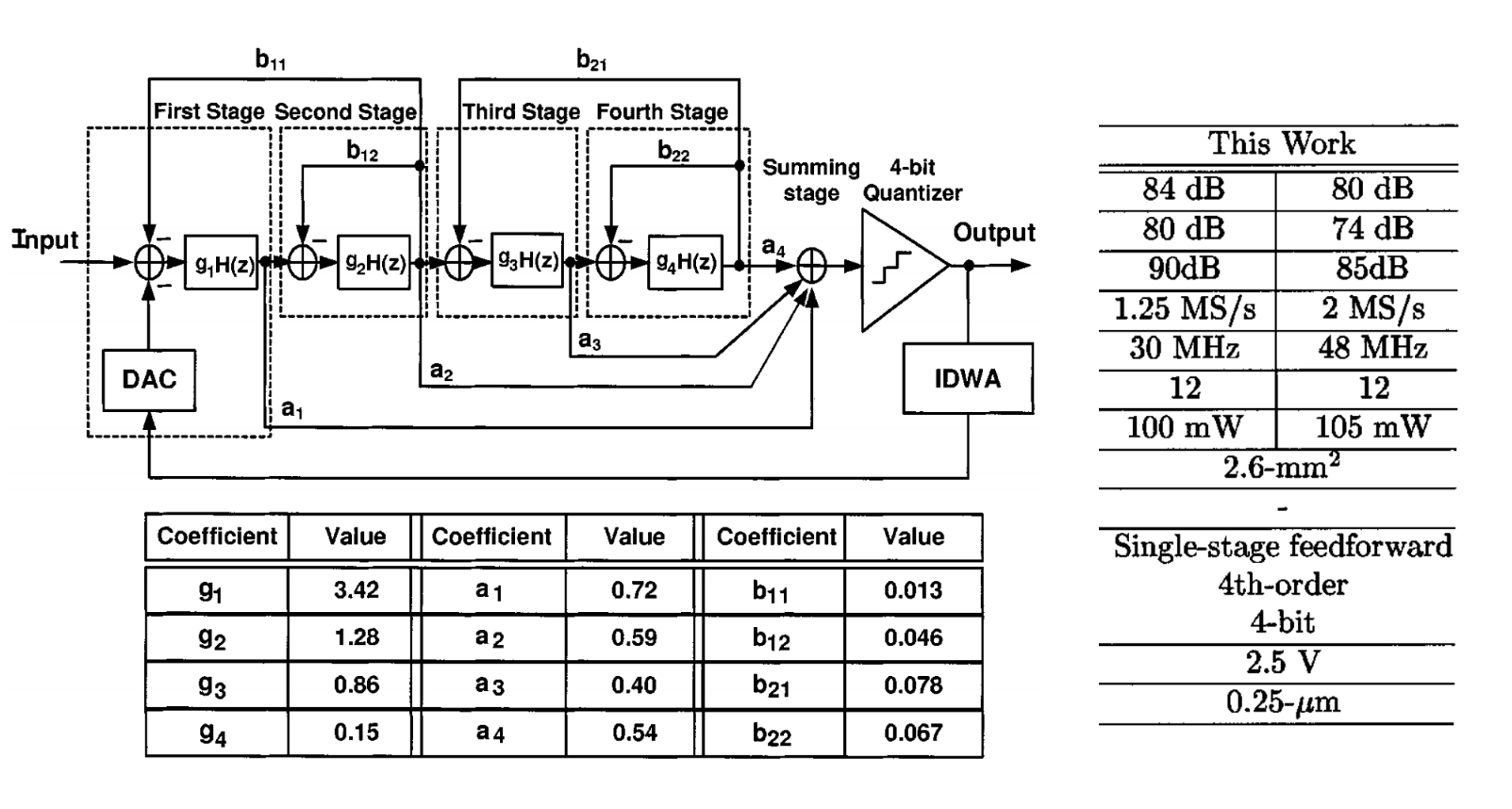
¶ 4.4 Rotated-DWA
这篇论文 "A 14-Bit Current-Mode DAC Based Upon Rotated Data Weighted Averaging" (JSSC, 2000) 提出的 RDWA (Rotated Data Weighted Averaging) 技术,是一种通过“牺牲部分底噪(Noise Floor)”来换取“无杂散动态范围(SFDR,即消除 Tone)”的技术。
传统的 DWA 可以想象成所有元件排成唯一的一个圆圈,指针一直在上面转。因为“圈”是固定的,如果输入信号有规律(比如 DC 或特定频率),指针的旋转轨迹就会产生固定的循环模式(Limit Cycle),从而产生 Tone。
RDWA的做法是:
- 准备多个“圈”:它不再只用一个固定的元件顺序,而是预先定义好了多个不同的“圈”(Circles)。每个“圈”里元件的排列顺序不同(相当于把元件序列做了“旋转”或重排)。
- 圈内正常转:在一个圈内,它依然像普通 DWA 一样工作(顺时针选元件,保证一阶噪声整形)。
- 随机跳圈 (Random Jumping):关键点在于,它不会一直死在一个圈里转。当指针停在某些特定位置(如偶数位置)时,它会随机地(Randomly)决定是继续在这个圈里跑,还是跳到另一个圈去跑。
随机这个过程会抬高底噪,论文中非常明确地讨论了这个权衡,并引入了一个关键参数:MTBS (Mean Time Between Switching,平均切换时间)。
- 如果跳得太频繁(MTBS 短):Tone 抑制好,但是规律被打得很散。因为“跳圈”本质上是一种随机扰动(注入了白噪声),跳得越快,注入的白噪声能量越大,底噪抬升越明显。
- 如果跳得太慢(MTBS 长):底噪低接近理想 DWA 的整形效果。因为在同一个圈里呆太久了,固定的规律又冒出来了,Tone 又会回来。
它的本质是在 “理想 DWA(低底噪但有 Tone)” 和 “完全随机 Dither(无 Tone 但高底噪)” 之间找了一个平衡点。通过控制 MTBS,设计者可以决定“多久跳一次”,从而在“消除 Tone”和“保持低底噪”之间进行微调。
¶ 4.5 Randomized DWA & Offset
这篇论文 "Techniques for Preventing Tonal Behavior of Data Weighted Averaging Algorithm in Modulators" (Vadipour, 2000) 主要提出了 两个 技术来解决 DWA 的 Tone 问题
OFFSET TECHNIQUE
DWA 的 Tone 问题(尤其是 那个大 Tone)通常发生在输入信号很小(接近 0)的时候,因为这时候主要在用 Code 4,导致指针转得非常有规律,Offset Technique 的做法是直接在输入信号上加一个固定的 DC Offset(例如 0.5 LSB)。优点是非常简单,不抬高底噪,甚至能改善 SNR(因为把带内 Tone 移走了)。缺点是对于本来就是测量 DC 信号的系统不适用(因为你改了输入值)。
Randomized DWA
这篇论文的重头戏是 Randomized DWA
- DWA 的核心规则是:“在所有元件都被用过一遍之前,任何元件都不能被重复使用。”(这样才能保证一阶整形)。传统的 DWA 为了省事,在这个规则下选择了“顺序轮询”(1,2,3 -> 4,5 -> 6,7,8...),然而正是这种“顺序”导致了 Tone。
- RnDWA 的改进:我们能不能遵守核心规则,但是“乱序”地选?比如要选 3 个:我不一定要选 {1,2,3},我可以选 {1,5,8},只要它们是“还没被用过”的就行。
为了硬件简单,论文提出了一种“部分随机化”的实现方法,平时还是像普通 DWA 一样顺序旋转(保持简单),每当完成一整圈循环(即所有元件都用过一遍了),我们就随机选一个新的起点(Random Pointer Reset),对于一个 8 element 的 RnDWA 的示例如下
| n | 反馈 | 使用的 Element | 起点 | 注释 |
|---|---|---|---|---|
| 0 | 1 | 初始化 | ||
| 1 | 4 | 1 2 3 4 | 1 | 正常轮巡 |
| 2 | 5 | 5 6 7 8 3 | 3 | 轮巡完一圈,从这次没有使用的 1 2 3 4 中随机挑出 3 |
| 3 | 2 | 4 5 | 3 | 正常轮巡 |
| 4 | 8 | 6 7 8 1 2 3 4 5 | 4 | 物理限制必须全选,从 1 2 3 4 5 但是有了新的起点 4 |
| 5 | 4 | 5 6 7 8 | 4 | 正常轮巡 |
| 6 | 2 | 1 2 | 4 | 正常轮巡 |
¶ 5 参考文献
- 1995_[DEM]_Schreier_Noise-shapedmultbit_DA_convertor_employing_unit_elements.pdf
- 1995_[DWA]_VLSI_Linearity_Enhancement_of_Multibit_ΣΔ_AD_and_DA_Converters_Using_Data_Weighted_Averaging.pdf
- 1996_[DEM]_Henderson_An_Anylsis_of_DEM_in_Sigma-Delta_Modulation.pdf
- 1996_[TI]_An_Audio_DAC_with_90dB_Linearity_using_MOS_to_Metal-Metal_Charge_Transfer.pdf
- 1998_[TI]_Some_Observations_on_Tone_Behavior_in_Data_Weighted_Averaging.pdf
- 1999_[IDWA]_An_Improved_Technique_for_Reducing_Baseband_Tones_in_Sigma_Delta_Modulators_Employing_Data_Weighted_Averaging_Algorithm_Without_Adding_Dither.pdf
- 2000_[BiDWA]_ISSCC_Cascaded_Multibit_AZ_Modulation_at_8x_osr.pdf
- 2000_[BiDWA]_JSSC_A_90-dB_SNR_2.5-MHz_Output-Rate_ADC_Using_Cascaded_Multibit_Delta_Sigma_Modulation_Oversampling_Ratio_at_8x_OSR.pdf
- 2000_[PartialDWA]_JSSC_A_Multibit_Delta_Sigma_Audio_DAC_with_120-dB_Dynamic_Range.pdf
- 2000_[RDWA]_JSSC_A_14-Bit_Current-Mode_DAC_Based_Upon_Rotated_Data_Weighted_Averaging.pdf
- 2000_[RnDWA]_Techniques_for_Preventing_Tonal_Behavior_of_Data_Weighted_Averaging_Algorithm_in_Modulators.pdf
- 2001_[PartitionedDWA]_JSSC_A_2.5-V_Sigma_Delta_Modulator_for_Broadband_Communications_Applications.pdf
- 2002_[IDWA]_JSSC_A_Wideband_CMOS_Sigma_Delta_Modulator_With_Incremental_Data_Weighted_Averaging.pdf
- 2004_[pseudo_DWA]High-Order_Multibit_Modulators_and_Pseudo_Data-Weighted-Averaging_in_Low-Oversampling_ADCs_for_Broad-Band_Applications.pdf
- 2007_[ADWA]_Advancing_Data_Weighted_Averaging_Technique_for_Multi-Bit_Sigma_Delta_Modulators.pdf