¶ 1 引言
关于系统稳定性,我们从《电路》的微分方程学到《自控》的根轨迹,再到《模电》的相位裕度。然而,当真正面对电路设计中的零极点对消(Pole-Zero Cancellation)或 Gain Boosting 的辅助运放设计时,这些孤立的理论往往让人感到困惑:为什么频响分析要扔掉 ?零点究竟如何影响瞬态?包含虚部的共轭零点/极点又如何影响瞬态?Pole-Zero Doublet 为何会恶化建立时间?明显感到这些理论背后有一套统一的机制,但教科书却往往分而治之。本文试图厘清这些似是而非的概念,挖掘理论背后的统一机制,为复杂的电路设计建立更深刻的直观理解。
其它相关内容:
- 深入理解微分方程的时域求解过程,非常有助于打破频域零极点与瞬态响应之间的理解障碍,详见 Time-Domain-Analysis-of-Linear-ODE
- 通过 Laplace 变换以及留数法(也叫Heaviside Cover-up Method),可以高效求解微分方程,利用这个方法可以分析 Pole-Zero Doublet 的影响详见 Pole-Zero-Doublet-Impact-on-Settling
- Miller 补偿已经成为模拟电路设计者的基本功,那么三级运放的稳定性补偿与直观理解同样重要,从波德图出发直观分析三级运放中最重要的两个补偿方式 NMC/MNMC 详见 Three-Stage-Amplifier-Stability-Compensation
¶ 2 系统的传递函数
一个连续线性时不变系统,通过 Laplace 变换分析,其传递函数可以写成如下形式
- Root-Locus Form 是控制理论和数学计算视角的标准形式:其一,根轨迹分析,比如分析运放的稳定性、PLL环路中,我们经常研究当增益 变化时,闭环极点会在复平面上如何移动。在这种分析下, 是唯一的变量,如果将系数 和后面的零极点混在一起就会变得非常麻烦;其二,可以很方便地看出高频 时系统的状态;其三:在进行部分分式展开求解 Inverse Laplace Transform 的时候,与公式表的形式对应
- Bode Form 在模拟电路设计中,通常关心DC增益(直流增益)和带宽非常直观
这里 ,是一个复数平面, 是让分子等于 0 的值,称之为零点; 是让分子等于 0 的值,称之为极点;通过他们的实部的正负,来判断他们处在左半平面还是右半平面,称之为为 RHP/LHP/LHZ/RHZ,对应的英文全称是 Right/Left Half Plane Pole/Zero
考虑一个 响应并增加一条前馈路径 的系统,列出节点的电压和电流关系
消去连接的桥梁, 和 ,只分析输入电压与输出电压在系统参数影响下的关系,就得到了微分方程:
将这个方程进行 Laplace 变换,可以继续得到复频域的传递函数:
从时域的视角去观察复频域的传递函数:
- ZIR 零输入响应: 这是系统内部存储的能量释放,存储在 和 上的初始电荷通过 释放到 0,因为此时是零输入;
- ZSR 零状态响应: 完全由输入驱动的响应,低频 时候,增益是 1;高频 时增益是 ,这就是为什么阶跃响应会有跳变,能量通过 这个“快速通道”瞬间分压到输出端
- 输入初始跳变修正项: 在 Laplace 变换中,阶跃输入信号 的复频域是 ,如果 ,即输入其实没有发生跳变,那 ZSR 中分子的快速前馈通路应该是不起作用的,这个修正项正好减去了这个跳变
¶ 3 系统稳定性分析
¶ 3.1 经典二阶阻尼系统
在控制与系统这门课中,二阶系统具有非常重要的作用,微分方程描述如下, 是输出; 是输入; (Zeta) 是阻尼比; 是自然频率(固有频率)
计算传递函数得到
这个分母 被称为特征多项式。它的根(极点)直接决定了系统的稳定性表现,和我们在时域上的齐次解是一一对应的,令分母为 0 求根:
只要 ,系统就是稳定的,意味着零输入响应下,输出总是衰减的
| 阻尼状态 (State) | 阻尼比条件 (ζ) | 极点特征 (Poles) | 物理/数学描述 |
|---|---|---|---|
| 过阻尼 (Overdamped) | 两个不相等的实数极点 | 根号内是正数,系统不震荡,响应较慢。 | |
| 临界阻尼 (Critically Damped) | 两个重合的实数极点 () | 根号内为 0,不发生震荡前提下最快回到稳态。 | |
| 欠阻尼 (Underdamped) | 一对共轭复数极点 () | 根号内是负数,出现虚数 ,系统会震荡。实部决定衰减速度,虚部决定震荡频率。 | |
| 无阻尼 (Undamped) | 极点在虚轴上 () | 对应 LC 永不停歇的等幅震荡。 |
¶ 3.2 相位裕度理论
主要目的是从开环传递函数,分析闭环传递函数的特性,为什么我们总是分析 0dB 的 Phase Margin,负反馈的机制是“做减法”,即输入减去反馈信号。如果一个正弦波信号在环路里跑了一圈,相移达到了 180°,它就变成了一个反相的波形(比如波峰变成了波谷)。这时候,“输入 - 反馈” 变成了 “输入 - (-反馈)”,也就是 “输入 + 反馈”。原本用来纠错的负反馈,瞬间变成了推波助澜的正反馈。如果此时环路增益 ,这个误差就会被无限放大,导致振荡发散。所以,180° 是“负反馈失效并转为正反馈”的临界线
接着观察开环到闭环的过程,假设开环传递函数是 ,在单位负反馈下,闭环传递函数就是
- 关于零点:开环的零点,直接就是闭环的零点, 你看 的分子依然是 乘以个系数。这意味着,如果你在开环里引入了一个零点,它会原封不动地出现在闭环传递函数里。这非常关键,因为零点代表了系统对某些频率成分的“微分”或“加速”作用,这个特性在闭环后依然保留
- 关于极点:开环的极点,只是闭环极点的“出发点” 的分母变成了 。这意味着闭环极点完全变了,它们不再是 的根,而是特征方程 的根。随着增益 K 的变化,闭环极点会从开环极点出发,沿着根轨迹移动。我们做零点频率补偿,本质上就是通过修改 和 ,来控制 的根尽量落在左半平面的实轴上。
Bode Plot
伯德图中,传函相乘,幅度响应相加;传函相加,幅度响应取决于更大的一个
| 类型 | 幅频特性 | 相频特性 | 稳定性影响 |
|---|---|---|---|
| 左半平面极点 (LHP Pole) | -20dB/dec | 滞后 (下降) -90° |
正常系统组成部分 |
| 右半平面极点 (RHP Pole) | -20dB/dec | 系统不稳定 | |
| 左半平面零点 (LHP Zero) | +20dB/dec | 超前 (上升) +90° | 增强稳定性 (增加相位裕度) |
| 右半平面零点 (RHP Zero) | +20dB/dec | 滞后 (下降) -90° | 削弱稳定性 (减小相位裕度,引起下冲) |
¶ 3.3 根轨迹
根轨迹仍然分析是闭环传递函数,分析的是如下方程的根,从 变换过程根轨迹的变化,总是开始于从开环极点(x)出发,终止于开环零点(o)
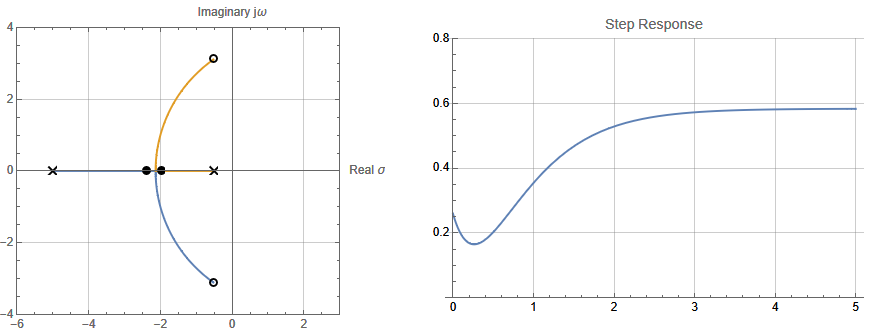
手绘有很多法则,但是利用工具会更加方便,如下图是利用 Mathematica 进行的根轨迹分析,开环极点(x)/开环零点(o)/ K=0.35(●)
- K=0.35 的时候闭环极点仍然处于实轴上,从齐次解的求解过程中,我们知道此时只有衰减项没有振荡项,观察其阶跃响应确实没有Overshoot;
- 根轨迹只分析闭环极点,不分析闭环零点,因为闭环零点不随 K 变化,但是我们实际分析系统的瞬态响应时,需要考虑零点的作用;阶跃刚开始,由于共轭零点的微分作用,并不是从0开始的,而是直接有了一个跳变,观察 时刻的 解释了这一点,初始态的跳变非常快,系统响应取决于高频增益,也就是
- 接下来我们发现阶跃响应有个下探的过程,而不是向着终值单调变化,这是因为 时刻的系统的零点决定的变化率 是负数,决定此后输出将会向下走;然后最终的 所以接下来会上扬并最终稳定(详细分析见后续章节 #5.1 零点作用过程分析)
ClearAll["Global`*"]
(* 1.定义开环/闭环传递函数 *)
L[s_, k_] := k*(s^2 + s + 10)/((s + 5/10)*(s + 5));
G[s_, k_] := L[s, k]/(1 + L[s, k]);
(* 2.绘制根轨迹 (Root Locus) *)
rlPlot = RootLocusPlot[L[s, k], {k, 0, 100},
PlotRange -> { {-6, 3}, {-4, 4} },
PoleZeroMarkers -> {"ParameterValues" -> {0.35} },
AxesLabel -> {"Real \[Sigma]", "Imaginary j\[Omega]"},
GridLines -> Automatic,
Frame -> True
]
(* 3.分析不同 K 值下的阶跃响应 *)
kvalue = 0.35;
system = TransferFunctionModel[G[s, kvalue], s];
response = OutputResponse[system, UnitStep[t], t];
Plot[response, {t, 0, 5}, PlotRange -> {0, 0.8},
PlotLabel -> "Step Response",
GridLines -> Automatic,
Axes -> True
]
(*4.计算y(0)=0.259,y'(0)=-0.864,y(∞)=0.583*)
y0 = Series[s*(1/s)*G[s, kvalue], {s, Infinity, 0}] // Normal
y0d = Series[s*(s*(1/s)*G[s, kvalue] - y0), {s, Infinity, 0}] // Normal
yinf = Series[s*((1/s)*G[s, kvalue]), {s, 0, 0}] // Normal
¶ 3.4 典型二阶系统根轨迹
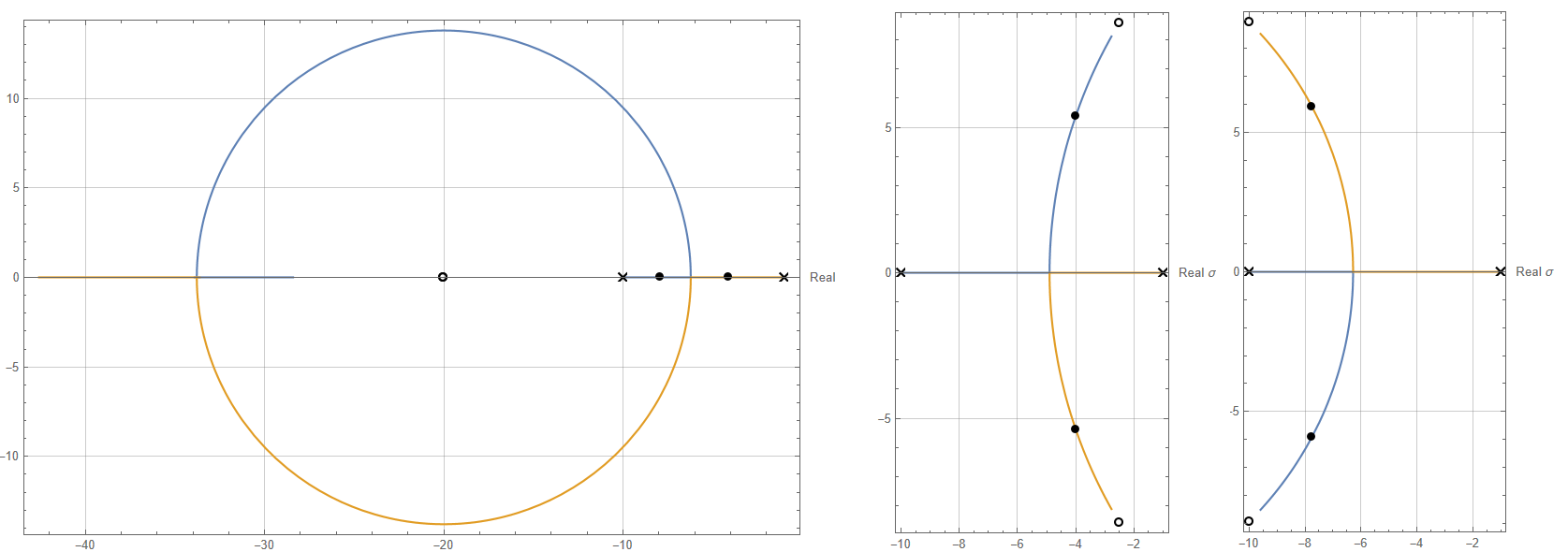
高频单零点(左图);共轭低频零点(中图);共轭高频零点(右图);
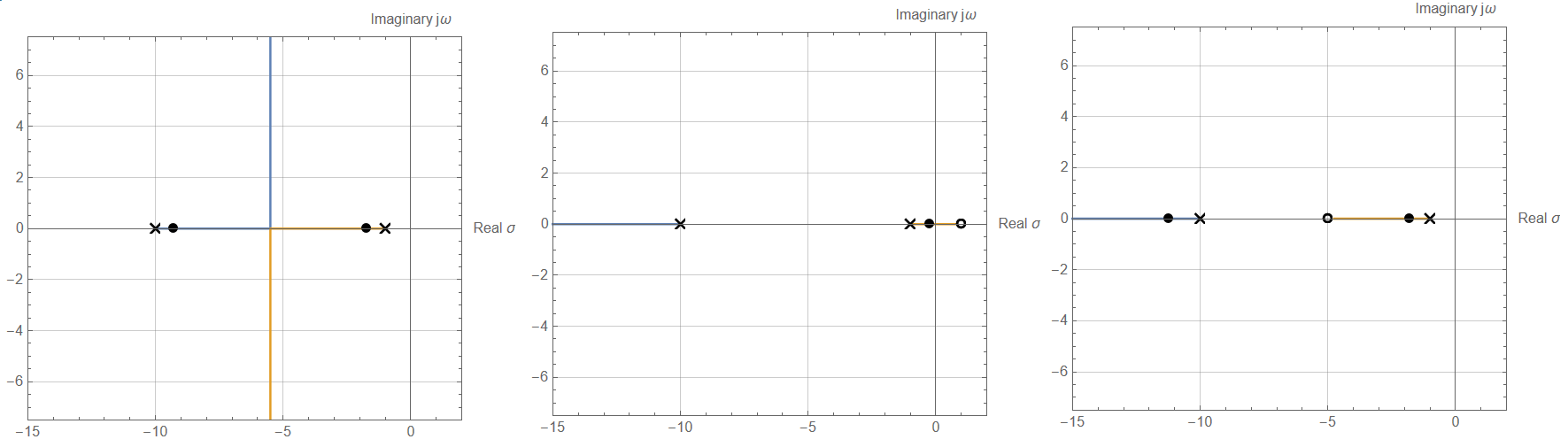
无零点(左图);单右零点(中图);单中频零点(右图);
¶ 4 极点与瞬态响应
¶ 4.1 齐次解与瞬态响应
闭环极点总是从开环极点出发,终止于开环零点(或无穷远处)。这意味着随着增益 增大,闭环系统的表现会越来越像零点及其附近的特性。如果根轨迹趋向于虚轴,系统变不稳定;如果趋向于零点,极点被零点“吸引”。极点就是系统微分方程的齐次解,所以理解齐次解,也就理解了极点的瞬态响应。
详见:Time-Domain-Analysis-of-Linear-ODE#2.2 理解齐次解的形式
极点(Poles)是系统的“体质”,闭环极点是特征方程 的根,它们定义了系统本质上“想”怎么运动。
- 实轴极点: 对应单调的指数衰减或增长。极点离虚轴越远(越向左),衰减越快,系统响应速度越快(时间常数 越小)。
- 复数极点: 必须共轭成对出现 ()。它们引入振荡分量。
- 实部 (): 决定收敛包络线的快慢。
- 虚部 (): 决定振荡的频率。
- 阻尼比 (): 极点与负实轴的夹角决定。夹角越大,阻尼越小,振荡越剧烈。
¶ 4.2 复极点夹角与阻尼系数
这里解释为什么阻尼比 () 由夹角决定,还记得共轭极点的特征方程,求解的根满足以下关系
所以实部是 ,虚部 ,把这个堪称三角形的画,那么斜边就是
那么在这个三角形当中,这个夹角的 正好就是 ζ
¶ 5 零点与阶跃响应
¶ 5.1 零点作用过程分析
直观理解零点的核心原理是 零点 = 导数项(微分控制),零点在微分方程中,是激励信号的导数产生的,作用是信号预测和相位超前。考虑一个二阶负反馈系统的传递函数:
开环DC增益为
初值: 初始是否产生跳变,取决于阶跃响应 是多少,根据初值定理
所以产生跳变是零点极点的个数相等(实际电路中零点≤极点恒成立),跳变大小取决于根轨迹传函形式下的 K 值
初始变化: 之后的趋势,取决于 的极性,应用拉普拉斯变换的微分性质和初值定理,可以得到
这样代入后,得到 的极性取决于(零点之和-极点之和)
- 对于具有 Complex LHP Zero 的系统,相比只具有实部的双零点,其 是一样的,但是 更大导致 DC 增益更高更不容易稳定;
- 对于的具有单个 RHP 零点的系统,开始一定或多或少有反向下探,利用二阶单零点系统里,为了保证负反馈,开环 DC 增益为正,k 一定是负数
高频零点作用时间:从初始变化率可以看出来,初始阶段的变化取决于极点和零点作用拉锯战中,粗略估算这个这个作用时间大约就就是零点带宽对应的时间常数
响应的终点:求解 需要用到终值定理,当然我们也可以通俗的理解为 DC 响应
这样自然得到如下表达式,通常 DC 增益 A 是一个远大于 1 的值
响应终点超调:一个系统的闭环极点仍然是 LHP 实数,LHP Zero 如果非常靠近甚至小于主机点的话,这也会造成超调 Overshoot;零点在微分方程中,是激励信号的导数产生的,作用是信号预测和相位超前;如果其作用时间范围 延申甚至接近到了主极点 ,在接近目标值仍然进行预测和相位超前,就造成了超调;
RHP Zero:首先明白零点的作用是预测,所以 RHP Zero 在相位是超前,但是其增益是反的,这就导致了它在故意使坏
¶ 5.2 造成零点的电路结构
LHP Real Zero: 这是“好”的零点,提供相位超前(Lead),增加系统阻尼,加快响应。 核心结构:串联的电阻-电容 (Series RC) 或 前馈通路与主通路“同相”叠加。
- 阻抗模型:ESR (等效串联电阻),最经典的例子是 LDO 或 DCDC 变换器的输出电容,即一个电容 串联一个寄生电阻 ,低频时电流走电容(积分,滞后);高频时电容短路,电流走电阻(比例,无滞后)。相位从 -90° 被拉回 0°,这就是 LHP 零点的“微分/预测”作用
- Miller 补偿中的 Rz,虽然可以理解其是为了限制 Cc 上的前馈电流 ,但是其前馈的电流在 R 上形成的 IR Drop,反而会进一步增强 ,甚至过补偿形成左零
- 另外一个是 MNMC 的中的快速的通路与慢速通路的叠加
RHP Real Zero:物理意义:这是“坏”的零点,提供幅值增益(+20dB/dec)但相位滞后(-90°)。导致“反向动作”(Non-minimum phase)。 核心结构:快通路与慢通路“反相”叠加。
- 米勒效应 (Miller Effect without Nulling Resistor),共源级 (Common Source) 放大器,栅极 (Gate) 和漏极 (Drain) 之间存在寄生电容 或补偿电容 ,构成了模拟 IC 设计中最著名的 RHP 零点来源;
- 慢通路 (主路径):,这是一个反相放大器 (Gain = )
- 快通路 (前馈路径):,高频下 阻抗变小,信号直接通过电容传过去。电容是双向导通的,它不反相。
- 主路径想把输出往下拉,前馈路径想把输出往上拉
- ,这就造成了你之前看到的 时刻的反向动作(前馈先到,主路径后到)
- Boost / Buck-Boost 变换器 (CCM 模式),这是电源设计中著名的“右半平面零点”,电感在输入和地之间切换
- 你需要输出电压升高 控制环路增加占空比
- 增加 开关管导通时间变长 电感充电时间变长
- 副作用:在这一周期内,二极管关断的时间(向负载提供能量的时间 )变短了!
- 这就是典型的 RHP 行为:我要去正向,但我必须先反向蓄力。
Complex Zeros:无论是 LHP 还是 RHP,复数零点都意味着 项,即电路中存在两个储能元件 (L+C 或 C+C) 的能量交换,或者是三条路径的叠加。
LHP Complex Zeros
- 陷波滤波器 (Notch Filter) / Twin-T 网络
- 在特定频率 ,两条并联路径的信号刚好幅度相等、相位相反,互相抵消,增益极小
- 这就是一对虚轴上的零点(或者靠得很近的 LHP 复零点)
- 这种滤波器,通常无法做到完全限制,让 ,由于寄生电阻或者 Charge Injection 构成的 1/FC 的电阻的存在,因此一定会造成一定的实部存在
- 前馈路径的二阶特性
- 如果你有一个主路径(增益1),和一个二阶高通路径(),它们同相叠加
- 。这就在 处产生纯虚数零点。如果稍加阻尼,就是 LHP 复零点
RHP Complex Zeros:相位极度滞后,幅值却有谐振峰。极其不稳定,极难补偿。 结构成因: 这种情况在常规单环路电路中很少见,通常出现在复杂的有源滤波器或多环路系统中。全通滤波器 (All-Pass Filter),全通滤波器不去左直连而是去构建滤波器,就是为了为了做延时或相位均衡,我们特意设计 ,这里分子就是一对 RHP 复数零点。
¶ 6. 伯德图 s 为什么替换成了 jω
¶ 6.1 瞬态与稳态
在分析系统的频率响应时,我们总是替换 s 传递函数中的 忽略了 ,解释这个之前,需要先明确两个概念:“系统的内特性决定的瞬态”和“外界激励维持的稳态”
- 极点中的 是特征方程的根,是内因,它描述的是如果你踢了系统一脚(冲击响应),然后不管它,它会怎么震荡和衰减。 决定了它自然衰减得有多快(阻尼); 决定了它自然震荡的频率;随着时间推移,因为有 ,这部分能量最终会耗尽。这就是瞬态响应 (Transient),随着时间推移会衰减消失的部分(由系统本身的特征极点决定)
- 频率响应的 是外因,当我们分析“频率响应”时,我们是在做一个特定的实验:用信号发生器给系统灌入一个纯正弦波,,这个信号没有衰减,因此 ;因为“频率响应”关注的不是系统受到冲击后的“自嗨”(瞬态),而是关注系统被迫跟随外部正弦波跳舞时的表现。这就是稳态响应 (Steady State),随着时间推移保留下来的部分(通常跟随输入的形态)。
当我们画波特图(Bode Plot)或分析频响时,我们默认已经等了足够久,瞬态早死光了。剩下还在动的,完全是由输入信号 维持的。所以,我们将传递函数 中的 替换为输入信号的特征 ,算出来的 就是在稳态下,输入正弦波被放大了多少倍。
¶ 6.2 几何直观理解 s 平面
那极点的 去哪了?既然 换成了 ,那极点的 依然在幕后起着决定性作用。我们从几何直观的角度,想象一下 s 平面 (S-Plane):
- 极点 (X):钉在 的位置不动。
- 扫描动作:频率响应分析,相当于你沿着 虚轴 ( axis) 从下往上走。你的坐标是 。
的作用是“距离”:当你的测试频率 慢慢增加,走到了 附近时(接近极点的虚部高度):
- 如果你离极点很近(即 很小):传递函数的分母 会变得很小,导致增益 暴涨。这就是谐振峰 (Resonance Peak)。
- 如果你离极点很远(即 很大):哪怕你走到了 旁边,由于水平距离 太大,分母依然很大,增益就不会有明显的尖峰。
- 同理零点导致的 Notch 也可以用以上 Pole-Peaking 的方式理解