1992年的 JSSC “A 100-MHz 100-dB Operational Amplifier with Multipath Nested Miller Compensation Structure” 中提出了这个理论,论文中的 “Fig.3 Bode plot of NMC structure” 明显画错了。好在 Johan Huijsing 在书里大体是正确的, “Operational Amplifier Theory and Design” 3rd Edition, 6.2.3 Three-GA-Stage Frequency Compensation,我们跟随作者的视角来直观理解三级运放的 NMC 和 MNMC 的频率补偿方法
Nested Miller Compensation (NMC),顾名思义,米勒嵌套补偿,首先像二级运放米勒补偿来补偿输出级和中间级(这两个级);其次,将中间级和输出级视为一个新的输出级,再次通过米勒补偿对整个放大器进行补偿。
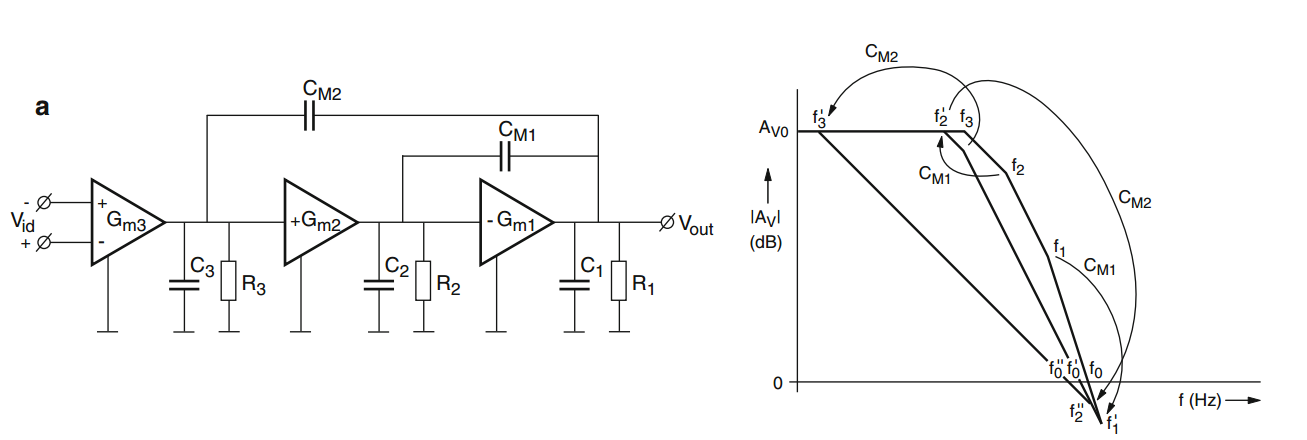
STEP1:先分析中间级和输出级,Cm1 将 f1 和 f2 分离到 f1' 和 f2',这是典型的弥勒作用
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧f1′=2π(C1+Cm1)gm1f2′=2π(Ro2)⋅(gm1Ro1Cm1+C2)1f0=2πCm1gm2
STEP2:接着 Cm2 将后两级短路,形成了单位增益运放,那么其内部的极点,低频的 f2‘ 转化为 Unite Gain Bandwidth, 移动到了非常高频的位置 f2'';原先较高频率的极点 f1' 将会往低频移动一些(根轨迹,接成闭环后,随着增益提高,闭环极点从开环极点出发,逐渐彼此靠近,相遇后朝上下移动),这部分图中没有画。同时 Cm2 形成的米勒电容,将 f3 移动到了非常低频的节点
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧f2′′≈2π(Ro2)⋅(gm1Ro1Cm1)(gm1Ro1)⋅(gm2Ro2)=2πCm1gm2=f0′f1′′=f1′−Δf3′=2π(Ro3)⋅(gm1Ro1gm2Ro2Cm2+C1)1f0′′=Cm2gm3(笔者见解,闭环后主极点确实就是GBW,但实际上 f2′′ 更高一点)(笔者见解,闭环极点根轨迹移动规律)
STEP3:保证主极点和次级点至少满足2倍关系,可以得到如下关系(原书中 6.37的公式再次写错)
f1′=2f0′=4f0′′⟹2πC1gm1=2×2πCm1gm2=4×2πCm2gm3
接下来我们用公式推导来证明上述的结论
ClearAll["Global`*"]
gds1 = 0;gds2 = 0;gds3 = 0;
eq1 = vi == -1;
eq2 = gm3*vi == (v3 - vo)*s*cm2 + v3*gds3;
eq3 = gm2*v3 == (v2 - vo)*s*cm1 + v2*gds2;
eq4 = -gm1*v2 + (v3 - vo)*s*cm2 + (v2 - vo)*s*cm1 == vo*s*c1 + vo*gds1;
Solve[{eq1, eq2, eq3, eq4}, {vo, v2, v3, vi}];
h = %[[1, 1, 2]] // FullSimplify
n = Collect[FullSimplify[Collect[Numerator[h], s]/(gm1*gm2*gm3)], s]
d = Collect[FullSimplify[Collect[Denominator[h], s]/(gm1*gm2*cm2*s)], s]
H(s)=−sCm2gm31+(gm2Cm1−gm1Cm1)s−gm1gm2C1Cm1s21−gm1Cm1s−gm1gm2Cm1Cm2s2≈−sCm2gm31+(gm1gm2Cm1(gm1−gm2))s+gm1gm2C1Cm1s21−gm1Cm1s−gm1gm2Cm1Cm2s2
从传递函数可以看到,需要保证 gm1>gm2 才能保证不出现右极点,如果 gm1/C1≫gm2/Cm1 那么分资可以简化为如下两个极点的形式,然而事实上两根之和比较小,而两根之积不变,意味着更接近正方形,所以中频极点会更高一些,高频极点会更低一点
D(s)=gm1gm2C1Cm1(s2+C1gm1−gm2s+C1Cm1gm1gm2)≈gm1gm2C1Cm1⋅中频极点 f2′′ 更大(s+Cm1gm2)⋅高频极点 f1′′ 更小(s+C1gm1)
再观察传递函数的分子,是存在一个左零和右零的,如果我们认为 Cm1 与 Cm2 大小相当,那么 gm2/Cm2<gm1/Cm1,如果认为有一个重根的话(几何平均数),那一次相为零;然而实际上两者之和为正,意味着 LHZ 会偏大一点
N(s)=−gm1gm2Cm1Cm2(s2+Cm2gm2s−Cm1Cm2gm1gm2)≈−gm1gm2Cm1Cm2⋅LHZ更大(1+(gm1gm2)/(Cm1Cm2)s)⋅RHZ更小(1−(gm1gm2)/(Cm1Cm2)s)
先右后左,幅值持续升高,但是相位先降再升;坏零点先起作用,但是这些零点一定在 GBW 以外,对主环路的PM 只会造成微不足道地衰减;至于后两级自身构成的二级Miller环路,略微补偿输出级的的零点,或许对于小环路的稳定有一定帮助;
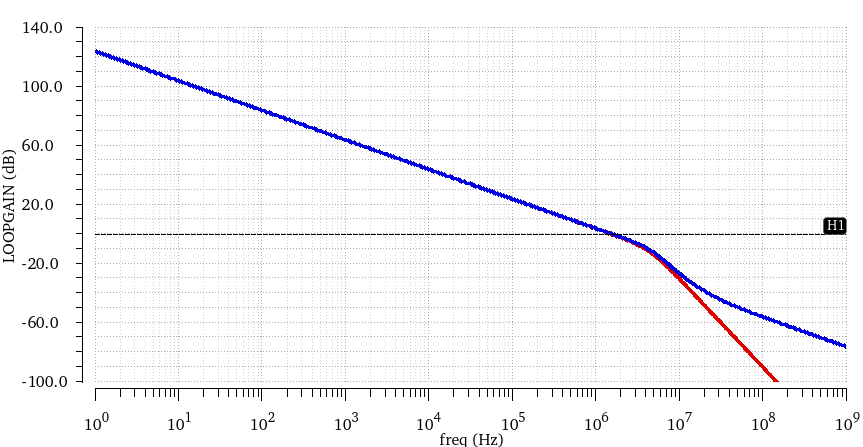
如下是 Macro Model 的对比仿真结果
- 红色利用VCVS实现 Buffer 单向传递的效果,彻底杜绝零点前馈
- 蓝色是包含前馈完整的 MNMC 的传递函数
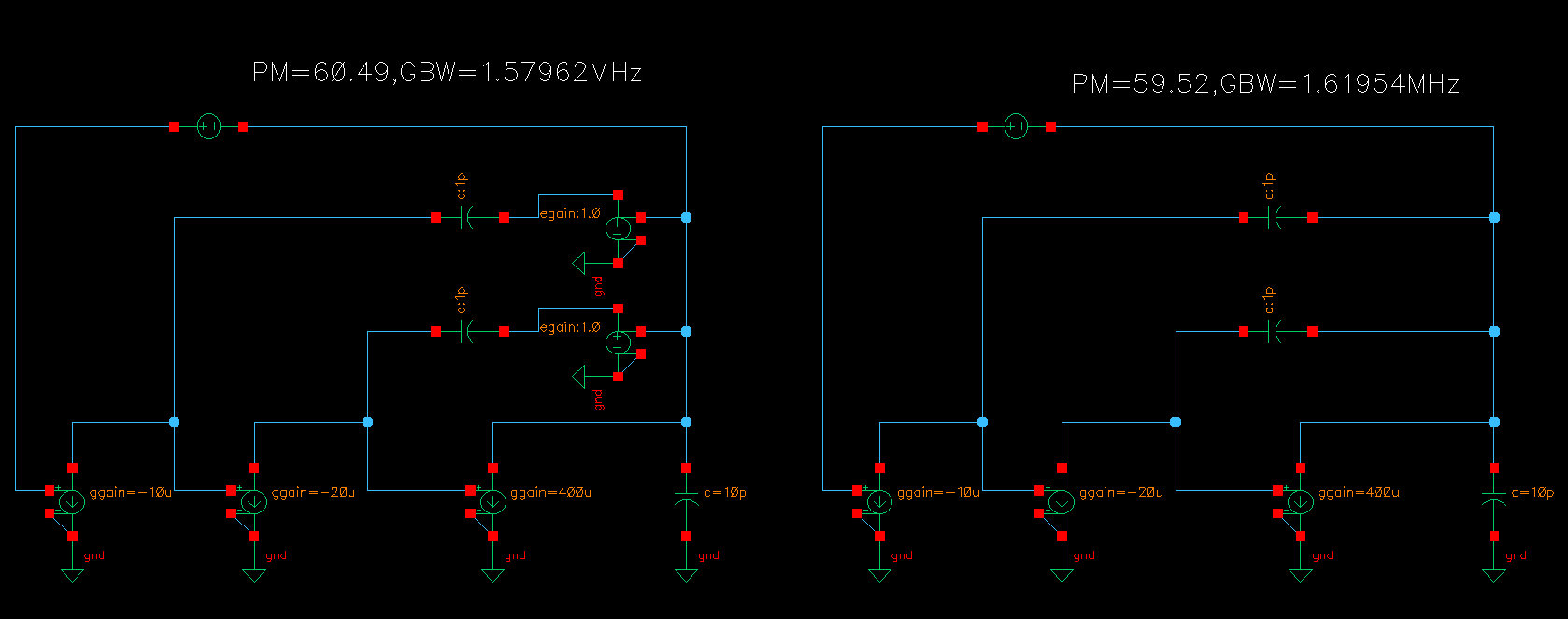
Multipath Nested Miller Compensation (MNMC),该电路具有第二个输入级,其跨导为 gm32,附加在具有 gm31 的第一输入级之上。第二个输入级形成了一条横跨第一输入级和中间级的独立并联路径。第二输入级的输出连接到输出级的输入端。事实上,我们有一个与三级放大器并联的额外两级放大器。在低频时,三级放大器凭借其巨大的低频增益占主导地位。但在高频时,两级放大器占主导地位。在中间范围内,两条路径具有相等的传递函数,但并未相加。
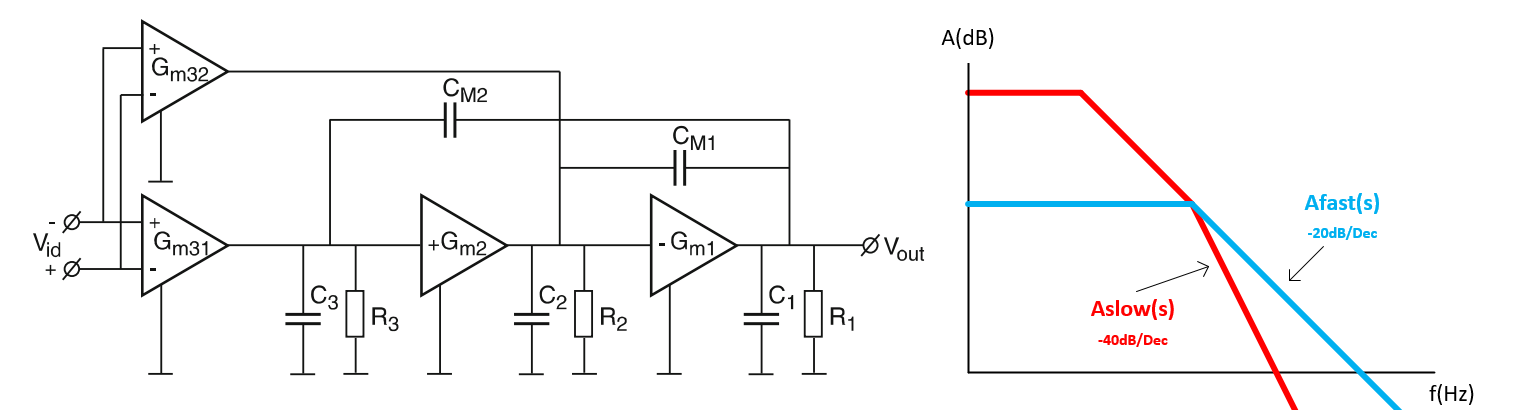
伯德图中,传函相乘,幅度响应相加;传函相加,幅度响应取决于更大的一个;我们的目标是接力,让三级运放开始 -40dB 滚降的点,恰好就是二级快速通路-20dB 滚降的点,完美衔接;也就是说 Afast 和 Aslow 相交的点正好就是三级运放开始变成 -40dB 滚降的点;显然易见,我们只需要让快通路的主极点等于慢通路的次级点即可。然而求蓝色 Afast(s) 主极点位置需要用到阻抗,非常麻烦,我们可以通过积分器近似的方法去求解,也就是让低频增益无限,我们只关注想要的频率范围的内幅度响应,这样
STEP1:快通路中频增益 Afast(s):快通路的路径是 gm32→gm1,如果我们只关注其 -20dB/Dec 这一段的话,那么其传递函数可以近似看作是一个一阶积分器
Afast,mid(s)=sCm1gm32
STEP2:慢通路中频增益 Aslow(s):慢通路的路径是 gm31→gm2→gm1 如果我们只关注其 -40dB/Dec 这一段的话,那么其传递函数可以近似看作是一个二阶积分器
Aslow,mid(s)=sCm2gm31sCm1gm2
STEP3:快通路=慢通路 找到交点所在的频率
Afast,mid(s)=Aslow,mid(s)⟹s0=gm32Cm2gm31gm2
STEP4:交点频率=慢通路次级点 得到设计需求
gm32Cm2gm31gm2=Cm1gm2⟹Cm2gm31=Cm1gm32
STEP5:Gm2退场位置 上面的步骤,我们只是得到中频段他们一定会相交,但是如果退场的位置太靠后,那这个快通路的主极点需要很高,接着对次级点的要求也提高了;这里我们并不希望其成为限制功耗的瓶颈
原次级点Cm1gm2≤⎝⎜⎜⎜⎛21C1gm1=Cm2gm31=快速通路GBWCm1gm32⎠⎟⎟⎟⎞⟹gm2≤gm32
从图中观察,我们希望退场位置在(原来的次级点)在快速二级放大器的 GBW 以内即可,Hujsing 给出的建议是取在 1/3 的位置,这样可以节省功耗。这个1/3充满了折衷,不仅考虑功耗,也考虑了 Pole-Zero Doublet,具体将在后续的数学推到中阐明
这里我们用一个小技巧,消除掉米勒电容的前馈路径,这些前馈路径造成的米勒前馈零点不是我们这里分析的重点
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧gm31Vi=sCm2(V3−Vo)+gds3V3gm2V3+gm32Vi=sCm1(v2−Vo)+gds2V2−gm1V2+sCm2(V3−Vo)+sCm1(V2−Vo)=Vo(sC1+gds1)gds1=gds2=gds3=0
这样得到的传递函数
H(s)=sCm2gm31⋅1+gm2/Cm1s+(gm2/Cm1)(gm1/C1)s21+(gm2gm31)/(gm32Cm1)s
从这个表达式,可以非常方便地看到三个极点以及前馈路径造成的零点
从这个当中,我们也观察到一个重要的问题,分母出现 gm2/Cm1 这个极点的前提,是 gm1/C1≫gm2/Cm1,事实上这个并不太可能;从 Doublet 的公式中,我们知道,其误差初值取决于零极点的匹配程度,而误差的衰减却取取决于 Doublet 的频率;困境来了,减小 gm2 可以让两者更加匹配,但又让频点降低,减缓衰减速度,Huijisng 的书中没有过多解释 gm2=gm32/3 的原因,或许直接从伯德图节省功耗的角度看,中间级确实越早退场越好;但是从瞬态响应的角度去看,这个 1/3 确实是个不错的选择。
y(t)≈闭环主极点响应1−e−ωut11−慢速拖尾(1−ωzωp)e−ωpt



