这份笔记旨在梳理线性时不变系统 (LTI System) 对应的微分方程求解流程。核心思想是将完全解 (General Solution) 分解为两部分:由系统自身特性决定的齐次解,和由外部输入决定的特解
对于一个 n 阶线性常微分方程 (Linear Ordinary Differential Equation, ODE):
andtndny+⋯+a1dtdy+a0y=f(t)
其完全解 (General Solution) y(t) 由两部分组成:
y(t)=Homogeneous Solutionyh(t)+Particular Solutionyp(t)
- Homogeneous Solution (齐次解 / 通解): 对应 Natural Response (自然响应) 或 Transient Response (瞬态响应)。令输入 f(t)=0 时系统的自由运动,只与系统本身的结构(特征根)有关。
- Particular Solution (特解): 对应 Forced Response (受迫响应)。由输入信号 f(t) 的形式决定,通常对应系统的稳态分量。
我们将特解代入,发现一定会满足方程,因为特解对应的系统达到的稳态;然而如果电路的初始态不是这样的稳态,达到这样的稳态经历了什么什么样的过程呢?电路的初态会让电路有什么样的行为呢?
由于我们分析的是线性方程,是可以做线性叠加的,在数学上,线性微分方程可以看作一个算子方程 L[y]=f(t),其中 L 是一个线性操作(比如求导、加权求和),y 是我们要找的解,f(t) 是方程右边的输入
L[yh+yp]=L[yh]+L[yp]=0+f(t)=f(t)
齐次解就是描述电路在初始状态下,在自身特性的作用下的一个响应过程
Step 1: 特征方程 (Characteristic Equation),将导数算子 dky/dtk 替换为 rk,得到代数方程:
anrn+⋯+a1r+a0=0
Step 2: 根据特征根 r 的性质,查表,写出对应的 yh(t):
| Case |
Roots |
Form of yh(t) (齐次解形式) |
Physical Meaning (物理含义) |
| Distinct Real Roots |
r1=r2 (实数) |
C1er1t+C2er2t |
Overdamped (过阻尼)
单调衰减 |
| Repeated Real Roots |
r1=r2=r (重根) |
(C1+C2t)ert |
Critically Damped (临界阻尼)
最快无超调衰减 |
| Complex Conjugate |
r=α±jβ |
eαt(C1cosβt+C2sinβt) |
Underdamped (欠阻尼)
振荡衰减 (α<0) |
Note: C1,C2 必须在求出特解并组合成全解后,利用初始条件求解
数学家们发现这类系统的解通常表现为指数增长或指数衰减(比如电路中的电容充放电、弹簧阻尼振动),比如模拟电路中的一阶 RC 的冲击响应就是 e−t/τ,将 −1/τ=r ,那么响应可以用更一般的形式给出来 ert;而这个这个响应有个特点,他的各阶导数分别是 ert, rert, r2ert…
那么对于一个 y′′(t)+y′(t)+y(t)=f(t) 的 ODE 来说,令激励 f(t)=0 观察系统固有的特性,代入我们大胆假设的方程,得到
r2ert+rert+ert=0
等号两边除以 ert 自然而然就得到这个特征方程
r2+r+1=0
- 如果求解得到的 r1,r2 是实数,带回完整的输入假设,自然得到 C1er1t+C2er2t
- 还是观察一阶 RC 这个电路,如果其输入信号为零,但是在电容上有一个初值2V,那么电容的电压衰减过程是 2e−t/τ,也就是说这里的 C1,2 其实代表了初值,高阶电路有几阶就需要几个初值
- 如果求解得到的是一个复数,那么通过欧拉公式 C1e(α+jβ)t+C1e(α−jβ)t=eαt(C1cosβt+C2sinβt)
- 如果求解得到的重根,那么得到就是 C1ert+C2ert=(C1+C2)ert
待定系数法 (Method of Undetermined Coefficients) 是最常用的工程方法。核心逻辑是:输出模仿输入 (Output mimics Input):
- 根据激励 f(t) 的形式,在映射表中找到特解的假设形式 yp(t)
- 代入导完成的方程中,求出待定系数 A,B…
- 如果初始假设特解 yp(t) ,也出现在了 yh(t) 中,就要应用 Modification Rule,修改特解的形式
| Input Signal f(t) (输入形式) |
Trial Particular Solution yp(t) (特解假设形式) |
Note |
| Constant K |
A |
A 是待定常数 |
| Polynomial tn |
Antn+⋯+A1t+A0 |
必须补全所有低阶项 |
| Exponential Keat |
Aeat |
指数系数 a 保持不变 |
| Sinusoid sin(ωt) or cos(ωt) |
Acos(ωt)+Bsin(ωt) |
必须同时包含 sin 和 cos 项 |
| Mixed eatcos(ωt) |
eat(Acosωt+Bsinωt) |
组合形式 |
我们要解的方程通常长这样
ay′′+by′+cy=f(t)
这意味着,特解 yp 必须是一个函数,当把它本身、它的一阶导数、它的二阶导数加权求和后,由于“巧合”(系数的抵消),最后剩下的东西刚好等于右边的 f(t),为了实现这种“抵消”,yp 必须和 f(t) 属于同一个函数家族。
-
指数函数 eat:
-
多项式 tn:
-
它的导数是 tn−1(降阶)。
-
如果你希望结果剩下 tn,那么特解里必须包含 tn。同时,为了抵消掉导数产生的 tn−1,tn−2...,特解必须把所有低阶项补全(Antn+⋯+A0)。
-
正弦/余弦函数:
-
sin(ωt) 的导数是 cos(ωt),再导又是 sin(ωt)。
-
它们是一对“孪生兄弟”。你不能只设 sin,因为方程左边可能有 y′ 项,会产生 cos。为了把这个多出来的 cos 抵消掉(因为右边可能只有 sin),你的特解必须一开始就包含 Acos+Bsin,让系数 A 和 B 去自动调节平衡。
映射表之所以是这样,是因为这些函数在求导后形式不变(或者只在有限的几个形式之间循环)。
如果输入信号的形式,恰好出现在了齐次解 yh(t) 中(即输入频率与系统固有频率重合),上述假设会失效(因为代入左边会变成 0)。修正法则是:在原假设基础上乘以 tk,直到它不再与齐次解重复。k 是特征方程中重根的重数。修正后的映射表如下
| 输入 f(t) |
特征根情况 (假设 r 为特征根) |
修正后的特解 yp(t) |
| Keat |
a 是单根 (r=a) |
A⋅t⋅eat |
| Keat |
a 是双重根 (r1=r2=a) |
A⋅t2⋅eat |
| cos(ωt) |
±jω 是共轭根 |
t[Acos(ωt)+Bsin(ωt)] |
在数学上,当你的输入信号 f(t) 的形式,恰好是对应齐次方程(让左边等于0)的解时,就发生了“谐振”。举一个最简单的例子
y′(t)+y(t)=e−t
特征根 r=−1,所以其次解就是 yh(t)=Ce−t;观察 f(t)=e−t 所以 Naive Guess yp(t)=Ae−t,与特征根是一样的,暂时不处理,直接代入方程左边,很显然结果是0,特征根方程干的就是这个事情。但是我们的目的是要让代入特解后,让左边等于右边的真实激励,从而求出系数 A,此时这个任务无法完成了。
⎩⎪⎨⎪⎧Left:Right:y′(t)+y(t)=−Ae−t+Ae−t=0f(t)=e−t
正确的做法是,依据 Modification Rule 乘以 t 后得到 yp(t)=tAe−t,代入方程左边得到
⎩⎪⎨⎪⎧Left:Right:y′(t)+y(t)=(Ae−t−tAe−t)+tAe−tf(t)=e−t
观察到 tAe−t 这项抵消了,这正是特征方程干的事情;但是在求导法则的作用下,前导后不倒的作用下,保留下来了 Ae−t 这个和 f(t) 一样形式的表达式,解出来来 A=1
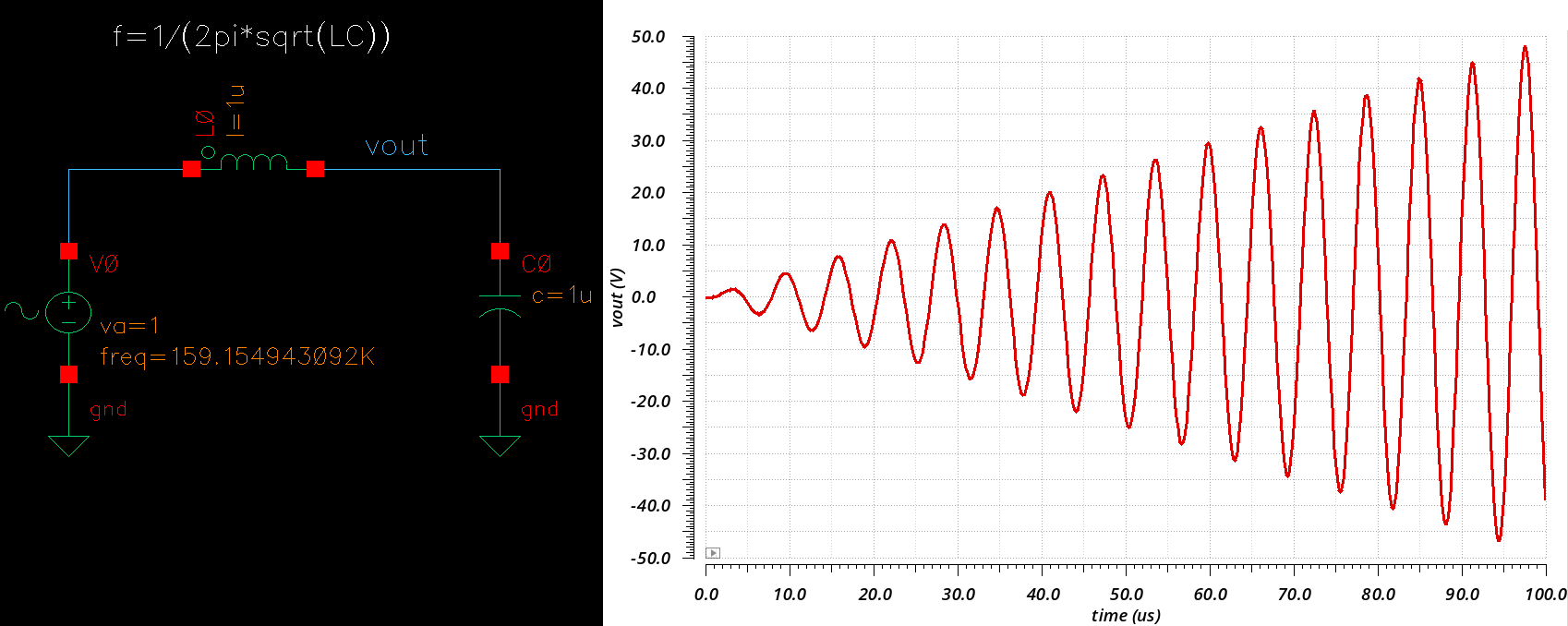
在电路层面,考虑一个 LC 响应,输出在 C 上,1/LC=ω, f(t)=sinωt
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧i(t)vind(t)f(t)=dtdy(t)=Ldtdi(t)=Ldtd(dtdy(t))=vind(t)+y(t)
这里一个小技巧是,利用输出电压得到 i(t),消去 i(t) 这个自变量,最终得到的微分方程
ω21y′′(t)+y(t)=f(t)
特征根是共轭复根,r=±j/LC=±jω,那么 Initial Guess of Particular Solution 是 yp(t)=Acos(ωt)+Bsin(ωt),代入方程左侧得到
⎩⎪⎪⎪⎨⎪⎪⎪⎧Left:Right:ω21(−Aω2cos(ωt)−Aω2sin(ωt))+(Acos(ωt)+Bsin(ωt))=0f(t)=sin(ωt)
这里方程左边等于0,无法求出待定的系数 A,B ,那么一个 f(t)=sin(ωt) 到底导致了一个什么样的输出呢?答案是 −(ωt/2)cos(ωt),也就是修正之后的形式,振荡的幅度是在线性增加,这个从 Cadence Spectre 仿真中得到了证实
Mathematica 中求导数简化计算的代码如下
ClearAll["Global`*"]
fp = A*t*Cos[\[Omega]*t] + B*t*Sin[\[Omega]*t];
left = D[D[fp, t], t]/(\[Omega]^2) + fp // FullSimplify
right = Sin[\[Omega]*t]
Solve[{left == right, B == 0}, {A, B}]
Solve the 2nd-order ODE,初始条件 y(0)=0,y′(0)=1:
y′′(t)+3y′(t)+2y(t)=4e−t
Characteristic Equation:
r2+3r+2=0⟹(r+1)(r+2)=0
Roots: r1=−1,r2=−2 (Distinct Real Roots).
yh(t)=C1e−t+C2e−2t
输入 f(t)=4e−t,很朴素地猜测特解应该是 yp(t)=Ae−t,但是我们发现这个和齐次解中的第一项相同,Resonance occurs (共振发生),需要进行修正,修正后的结果得到
yp(t)=A⋅t⋅e−t
计算各阶导数:
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧yp(t)yp′(t)yp′′(t)=Ate−t=Ae−t−Ate−t=A(1−t)e−t=−Ae−t−(Ae−t−Ate−t)=A(t−2)e−t
这里用到了2个基本的求导公式
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧(f1(t)f2(t))′(f1(f2(t))′=f1′(t)f2(t)+f1(t)f2′(t)=df2(t)df1(f2(t))dtdf2(t)前导后不导+后导前不导将内部看作自变量整体求导,乘以内部的导数
将特解代入到原始的常微分方程中,求出系数 A
[A(t−2)e−t]+3[A(1−t)e−t]+2[Ate−t]=4e−tAe−t[(t−3t+2t)+(−2+3)]=4e−tAe−t[0⋅t+1]=4e−tA=4
得到 particular solution
yp(t)=4te−t
Combine yh and yp:
y(t)=C1e−t+C2e−2t+4te−t
初始条件必须代入全解计算,不能只代入齐次解
初始条件 y(0)=0 可以得到 Eq.1
y(0)=C1e0+C2e0+0=0⟹C1+C2=0(Eq.1)
第二个初始 y′(0)=1 可以得到 Eq.2
y′(t)=−C1e−t−2C2e−2t+4(1−t)e−ty′(0)=−C1−2C2+4=1−C1−2C2=−3(Eq.2)
这样可以得到 C1=−3, C2=3,最终结果如下
y(t)=−3e−t+3e−2t+4te−t
