Kamath, Meyer, and Gray 在 1974 年发表了关于运放建立时间的论文:Relationship Between Frequency Response and Settling Time of Operational Amplifiers
通常大家直觉认为:极点和零点离得很近(Doublet),应该就抵消了呀?残酷的现实是: 只要没有完全重合(Mismatch),它们就会在时域响应中产生一个幅度很小、但是衰减极慢的分量。这在普通精度下(如 1%)看不出来,但在高精度(如 0.1%, 0.01%)设计中,这个“长尾巴”会导致建立时间从几十纳秒暴增到几微秒甚至毫秒。
核心结论,Pole-Zero Doublet(极零点对偶)对阶跃响应的影响可以概括为:
y ( t ) ≈ 1 − e − ω u t 1 1 ⏟ 闭环主极点响应 − ( 1 − ω p ω z ) e − ω p t ⏟ 慢速拖尾 y ( t ) ≈ 闭环主极点响应 1 − e − ω u t 1 1 − 慢速拖尾 ( 1 − ω z ω p ) e − ω p t
ω u ω u ω p , z ω p , z 虽然 ( 1 − ω p / ω z ) ( 1 − ω p / ω z ) ω p , z ω p , z
为了看清本质,我们将系统简化为一个二阶系统:包含一个开环增益 A A ω d ω d ω p ω p ω z ω z
H ( s ) = A ( 1 + s / ω z ) ( 1 + s / ω d ) ( 1 + s / ω p ) H ( s ) = ( 1 + s / ω d ) ( 1 + s / ω p ) A ( 1 + s / ω z )
那么闭环传递函数
G ( s ) = H ( s ) 1 + H ( s ) = A ( 1 + s / ω z ) A ( 1 + s / ω z ) + ( 1 + s / ω d ) ( 1 + s / ω p ) G ( s ) = 1 + H ( s ) H ( s ) = A ( 1 + s / ω z ) + ( 1 + s / ω d ) ( 1 + s / ω p ) A ( 1 + s / ω z )
将分母展开,得到
D ( s ) = 1 ω d ω p s 2 + ( 1 ω d + 1 ω p + A ω z ) s + ( A + 1 ) D ( s ) = ω d ω p 1 s 2 + ( ω d 1 + ω p 1 + ω z A ) s + ( A + 1 )
继续化简,分解因式
ω d ω p D ( s ) = s 2 + ( ω d + ω p + A ω d ω p ω z ) s + ω d ω p ( A + 1 ) ω d ω p D ( s ) ∣ ω p / ω z = 1 = ( s + ( A + 1 ) ω d ) ( s + ω p ) ω d ω p D ( s ) = A ω d ω p ( 1 + s ( A + 1 ) ω d ) ( 1 + s ω p ) ⟹ D ( s ) = ( A + 1 ) ( 1 + s ( A + 1 ) ω d ) ( 1 + s ω p ) ω d ω p D ( s ) ω d ω p D ( s ) ∣ ∣ ∣ ω p / ω z = 1 ω d ω p D ( s ) ⟹ D ( s ) = s 2 + ( ω d + ω p + A ω d ω z ω p ) s + ω d ω p ( A + 1 ) = ( s + ( A + 1 ) ω d ) ( s + ω p ) = A ω d ω p ( 1 + ( A + 1 ) ω d s ) ( 1 + ω p s ) = ( A + 1 ) ( 1 + ( A + 1 ) ω d s ) ( 1 + ω p s )
将化简后的分母代入到方程当中,得到简化的二阶闭环传递函数,这里令 ω u = ω d ( A + 1 ) ω u = ω d ( A + 1 ) ω u ω u
G ( s ) ≈ A A + 1 ( 1 + s / ω z ) ( 1 + s / ω u ) ( 1 + s / ω d ) ≈ ( 1 + s / ω z ) ( 1 + s / ω u ) ( 1 + s / ω d ) G ( s ) ≈ A + 1 A ( 1 + s / ω u ) ( 1 + s / ω d ) ( 1 + s / ω z ) ≈ ( 1 + s / ω u ) ( 1 + s / ω d ) ( 1 + s / ω z )
输入为单位阶跃 U ( s ) = 1 s U ( s ) = s 1 Y ( s ) Y ( s )
Y ( s ) = G ( s ) U ( s ) = 1 s ⋅ ω p ω u ω z ⋅ s + ω z ( s + ω p ) ( s + ω u ) Y ( s ) = G ( s ) U ( s ) = s 1 ⋅ ω z ω p ω u ⋅ ( s + ω p ) ( s + ω u ) s + ω z
部分分式展开 (Partial Fraction Expansion),在数学上如果分母是几个互不相同的一阶因子(Distinct Linear Factors)相乘,那么它一定可以被唯一地拆解为几个简单的分数之和。 每一个分母因子,对应拆解后的一项。我们将 Y ( s ) Y ( s )
Y ( s ) = A s + B s + ω p + C s + ω u Y ( s ) = s A + s + ω p B + s + ω u C
我们需要求解系数 A , B , C A , B , C
求解系数 A ,遮盖住 Y ( s ) Y ( s ) s s s = 0 s = 0
A = 1 s ⋅ ω p ω u ω z ⋅ s + ω z ( s + ω p ) ( s + ω u ) ∣ s = o = 1 A = s 1 ⋅ ω z ω p ω u ⋅ ( s + ω p ) ( s + ω u ) s + ω z ∣ ∣ ∣ ∣ ∣ s = o = 1
接着求解系数 B,遮盖住 Y ( s ) Y ( s ) s + ω p s + ω p s = − ω p s = − ω p
B = 1 s ω p ω u ω z s + ω z ( s + ω p ) ( s + ω u ) ∣ s = − ω p = − ω u ω z ω z − ω p ω u − ω p B = s 1 ω z ω p ω u ( s + ω p ) ( s + ω u ) s + ω z ∣ ∣ ∣ ∣ ∣ s = − ω p = − ω z ω u ω u − ω p ω z − ω p
通常 Doublet 的频率远低于主带宽,即 ω p ≪ ω u ω p ≪ ω u ω u − ω p ≈ ω u ω u − ω p ≈ ω u
B ≈ − ω u ω z ω z − ω p ω u = − ω z − ω p ω z = − ( 1 − ω p ω z ) B ≈ − ω z ω u ω u ω z − ω p = − ω z ω z − ω p = − ( 1 − ω z ω p )
接着求解系数 C,遮盖住 Y ( s ) Y ( s ) s + ω u s + ω u s = − ω u s = − ω u
C = 1 s ω p ω u ω z s + ω z ( s + ω p ) ( s + ω u ) ∣ s = − ω u = − 1 ω u ω p ω u ω z − ω u + ω p − ω u + ω p C = s 1 ω z ω p ω u ( s + ω p ) ( s + ω u ) s + ω z ∣ ∣ ∣ ∣ ∣ s = − ω u = − ω u 1 ω z ω p ω u − ω u + ω p − ω u + ω p
通常 Doublet 的频率远低于主带宽,即 ω p , z ≪ ω u ω p , z ≪ ω u ω p / ω p ≈ 1 ω p / ω p ≈ 1
C = − 1 C = − 1
对展开式做拉普拉斯逆变换:
y ( t ) = L − 1 { 1 s + − ( 1 − ω p ω z ) s + ω p + − 1 s + ω u } = 1 − e − ω u t 1 1 ⏟ 闭环主极点响应 − ( 1 − ω p ω z ) e − ω p t ⏟ 慢速拖尾 y ( t ) = L − 1 ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ s 1 + s + ω p − ( 1 − ω z ω p ) + s + ω u − 1 ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ = 闭环主极点响应 1 − e − ω u t 1 1 − 慢速拖尾 ( 1 − ω z ω p ) e − ω p t
1990年的 JSSC "A Fast-Settling CMOS Op Amp for SC Circuits with 90-dB DC Gain" 的这篇论文首次系统性地分析了 Gain Boosting 引入的 Pole-Zero Doublet 对建立时间(Settling Time)的影响,并明确画出了辅助运放 GBW 的“安全窗口
下限:大于主环路的GBW,避免 pole-zero doublet 落在带内
上限:小于辅助环路的次级点,通常是 Cascode 管的源极的 gm 与 Cg 形成,保证小环路稳定
论文没有用公式推导,而是基于一些常用的结论,通过伯德图去直观地分析,这个正是模拟设设计者所需的素养,这里做一些 translation/rephrase 的工作
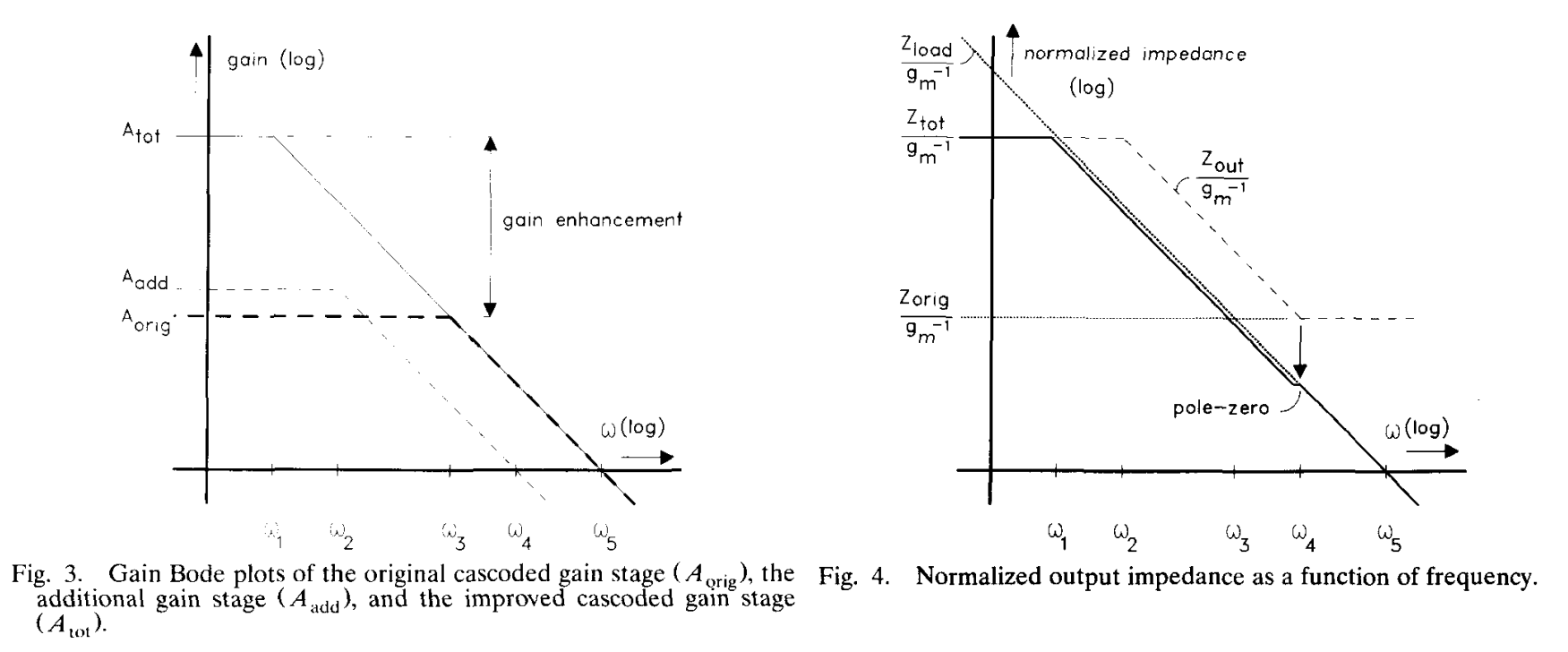
Fig. 3 展示了原始共源共栅增益级 (Aorig)、额外增益级 (Aadd) 和改进后的共源共栅增益级 (Atot) 的波特图。在直流处,根据公式,增益增强 Atot/Aorig 大约等于 [1+Aadd(0)]。对于 ω>ω1,输出阻抗主要由 Cload 决定。这导致 Atot(ω) 呈现一阶滚降。此外,这意味着只要 ω2>ω1, Aadd(ω) 在 ω>ω2 时可以有一阶滚降。这等同于一个条件:额外增益级的单位增益频率 (ω4) 必须大于原始级的3-dB带宽 (ω3),但它可以远低于原始级的单位增益频率 (ω1)。改进后的增益级和原始增益级的单位增益频率是相同的。
根据公式推导,增益增强技术将输出阻抗 Zout 增加了约 (Aadd+1) 倍。额外级的增益 Aadd 在频率高于 ω2 时以 -20 dB/十倍频程的斜率下降(Fig.3)。对于高于 ω4 的频率,Aadd 小于1,此时没有增益增强的共源共栅级的正常输出阻抗 Zorig 依然存在。这显示在 Fig.4 中。同时也显示了负载电容的阻抗 Zload 以及在输出节点形成总阻抗 Ztot 的并联电路。仔细观察该图可以发现,在 ω4 附近的总输出阻抗图中存在一个偶极子(doublet)。众所周知,由于慢建立分量的存在,偶极子会严重降低运放的建立行为。
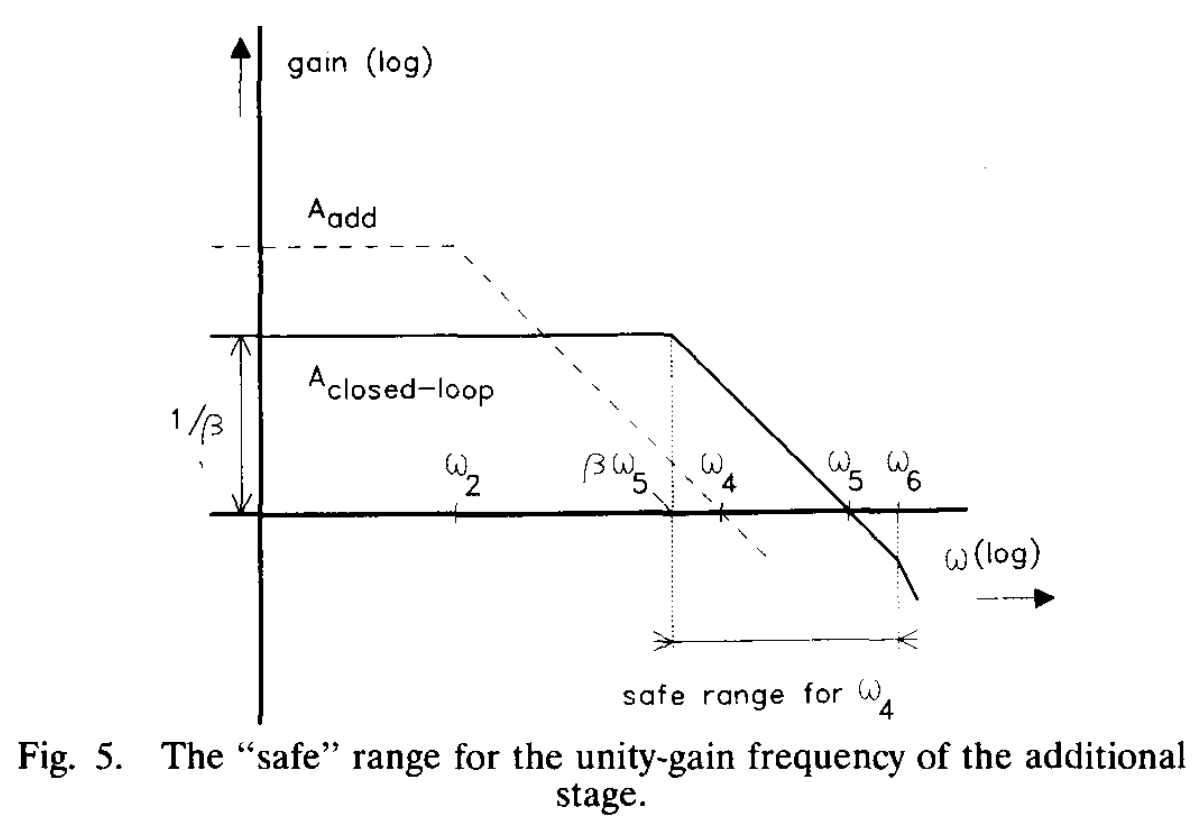
我们的方法是让这个“慢”建立分量变得足够快。如果偶极子的时间常数 1/ωpz 小于闭环(反馈因子为 β)的主时间常数 1/(βωunity),建立时间将不会因偶极子而增加。当额外级的单位增益频率高于电路的 -3-dB 带宽时,即可实现这种情况。另一方面,出于稳定性的考虑,单位增益频率必须低于公式(3)所指示的主放大器的第二极点频率。这导致了额外级单位增益频率的“安全”区域:
β ω 5 < ω 4 < ω 6 β ω 5 < ω 4 < ω 6
如 Fig.5 所示。注意这个安全区域比公式(3)给出的要小。然而,一个令人满意的实现并不成问题,因为决定 ω4 的额外级的负载电容远小于决定 ω5 的运放负载电容。 这很容易实现。综上所述,我们可以得出结论:增益增强技术的重复使用实现了运放直流增益与单位增益频率的解耦(decoupling)
Cascode 可以提高输出阻抗,Gain -Boosting 可以进一步提高输出阻抗
r o 1 ⏟ 单管阻抗 → g m 2 r o 2 r o 1 + r o 1 + r o 2 ⏟ Cascode 阻抗 → A g m 2 r o 2 r o 1 + g m 2 r o 2 r o 1 + r o 1 + r o 2 ⏟ Gain-Boosting 阻抗 单管阻抗 r o 1 → Cascode 阻抗 g m 2 r o 2 r o 1 + r o 1 + r o 2 → Gain-Boosting 阻抗 A g m 2 r o 2 r o 1 + g m 2 r o 2 r o 1 + r o 1 + r o 2
因此 Gain Boosting 的核心作用是提高输出阻抗,主运放的开环增益直接正比于这个阻抗
H ( s ) ≈ G m s C L + 1 R o u t ( s ) H ( s ) ≈ s C L + R o u t ( s ) 1 G m
但是这个辅助运放的带宽并不是无限的,这里我们引入具有单极点 ω p ω p A C ( s ) A C ( s )
R o u t ( s ) ≈ ( g m 2 r o 2 r o 1 ) ⋅ ( 1 + A C ( s ) ) = R 0 ( 1 + A C 0 1 + s / ω p ) ⏟ 同向且具有相位差会造成左零 = R 0 ( 1 + A C 0 ) ( 1 + s ( 1 + A C 0 ) ω p 1 + s ω p ) ≈ A C 0 R 0 1 + s / ( A C 0 ω p ) 1 + s / ω p R o u t ( s ) ≈ ( g m 2 r o 2 r o 1 ) ⋅ ( 1 + A C ( s ) ) = R 0 同向且具有相位差会造成左零 ( 1 + 1 + s / ω p A C 0 ) = R 0 ( 1 + A C 0 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ 1 + ω p s 1 + ( 1 + A C 0 ) ω p s ⎠ ⎟ ⎟ ⎟ ⎟ ⎞ ≈ A C 0 R 0 1 + s / ω p 1 + s / ( A C 0 ω p )
g m 2 r o 2 r o 1 g m 2 r o 2 r o 1 R 0 R 0 g m 2 r o 2 g m 2 r o 2 A C ( s ) A C ( s ) g m 2 r o 2 ⋅ ( 1 + A C ( s ) ) ⋅ r o 1 g m 2 r o 2 ⋅ ( 1 + A C ( s ) ) ⋅ r o 1 A C ( s ) A C ( s )
上面我们证明了主运放的开环增益 R o u t ( s ) R o u t ( s ) A C 0 ω p A C 0 ω p
更方便的,我们可以从开环传递进行分析
H ( s ) = G m R 0 A C 0 1 + s A C 0 ω p ( R 0 C L ω p ) s 2 + ( A C 0 R 0 C L + 1 ω p ) s + 1 H ( s ) = G m R 0 A C 0 ( ω p R 0 C L ) s 2 + ( A C 0 R 0 C L + ω p 1 ) s + 1 1 + A C 0 ω p s
这里,分析分母的 s s A C 0 R 0 C L A C 0 R 0 C L
p 1 = 1 A C 0 R 0 C L p 1 = A C 0 R 0 C L 1
次级点的位置用 A s 2 + B s + C A s 2 + B s + C s 1 ⋅ s 2 = C / A s 1 ⋅ s 2 = C / A
1 A C R 0 C L ⋅ p 2 = ω p R 0 C L ⟹ p 2 = A C 0 ω p A C R 0 C L 1 ⋅ p 2 = R 0 C L ω p ⟹ p 2 = A C 0 ω p
然而这里这里的 p 1 + p 2 p 1 + p 2 p 1 ⋅ p 2 p 1 ⋅ p 2 p 1 p 1 p 2 p 2
1 A C 0 R 0 C L − ⏟ 主极点 ≪ 1 A C 0 ω p ⏟ Doublet零点 ≤ 1 A C 0 ω p + ⏟ Doublet极点 主极点 A C 0 R 0 C L 1 − ≪ Doublet 零点 A C 0 ω p 1 ≤ Doublet 极点 A C 0 ω p 1 +
所以论文中 Fig.4 给出的伯德图非常准确,先看到零点,再看到极点,因此开环增益曲线从 -20dB/Dec 滚降,再到短暂的 0dB/Dec 的维持,接着很快回到 -20dB/Dec 滚降
现在我们把主运放接成闭环,反馈系数是 β β
G ( s ) = H ( s ) 1 + β H ( s ) = 1 β ( s A C 0 ω p + 1 ) ( C L G m β A C 0 ω p ) s 2 + ( C L G m β + 1 A C 0 ω p + 1 β G m R 0 A C 0 ω p ) s + ( 1 + 1 β G m R 0 A C 0 ) G ( s ) = 1 + β H ( s ) H ( s ) = β 1 ( G m β A C 0 ω p C L ) s 2 + ( G m β C L + A C 0 ω p 1 + β G m R 0 A C 0 ω p 1 ) s + ( 1 + β G m R 0 A C 0 1 ) ( A C 0 ω p s + 1 )
做一些符号简化工作
{ A 0 = G m R 0 (原主运放的开环增益) ω u = G m C L (原主运放的增益带宽积) ω u c = A C 0 ω p (辅助运放的增益带宽积) A t o t a l = A 0 A C 0 (Gain-Boosting 之后的总增益) ⟹ G ( s ) = 1 β ( s ω c u + 1 ) ( 1 β ω u ω c u ) s 2 + ( 1 β ω u + 1 ω c u + 1 β A 0 ω c u ) s + ( 1 + 1 β A t o t a l ) ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ A 0 = G m R 0 ω u = C L G m ω u c = A C 0 ω p A t o t a l = A 0 A C 0 ( 原主运放的开环增益 ) ( 原主运放的增益带宽积 ) ( 辅助运放的增益带宽积 ) (Gain-Boosting 之后的总增益 ) ⟹ G ( s ) = β 1 ( β ω u ω c u 1 ) s 2 + ( β ω u 1 + ω c u 1 + β A 0 ω c u 1 ) s + ( 1 + β A t o t a l 1 ) ( ω c u s + 1 )
这里我们认为 A t o t a l = A C 0 A 0 A t o t a l = A C 0 A 0 A 0 A 0 ω c u ω c u β ω u β ω u
G ( s ) ≈ 1 β ( s ω c u + 1 ) ( 1 β ω u ω c u ) s 2 + ( 1 β ω u + 1 ω c u + 1 β A 0 ω c u ) s + ( 1 + 1 β A t o t a l ) = 1 β ( s ω c u + 1 ) ( s β ω u + 1 ) ( s ω c u + 1 ) G ( s ) ≈ β 1 ( β ω u ω c u 1 ) s 2 + ( β ω u 1 + ω c u 1 + β A 0 ω c u 1 ) s + ( 1 + β A t o t a l 1 ) ( ω c u s + 1 ) = β 1 ( β ω u s + 1 ) ( ω c u s + 1 ) ( ω c u s + 1 )
我们从根轨迹的知识中证实了这一点,随着增益 K 从 0 变化到 ∞,闭环极点起始于开环极点,终止于闭环零点;然而显示情况是,增益 K 不是无穷大,或者说这里的 A 0 A 0 1 / ( β A 0 ω u ) 1 / ( β A 0 ω u )