¶ 二阶 FIR 传函零点
这里推到 3-Tap FIR 与 Notch 点的关系,通过这里的推到,将会得到 Understanding-FIR-Filter-Using-Factorization 的猜想,即满足 这种形式时,这里的 是一个实数,通过改变 可以调整 Null 的频率
在 Understanding-FIR-Filter-Using-Factorization 中,得到如下 2-Tap 或者 3-Tap 级联的滤波器,我们观察到存在3个 Null 点,而如下公式的第二排恰好有3个 这样的形式
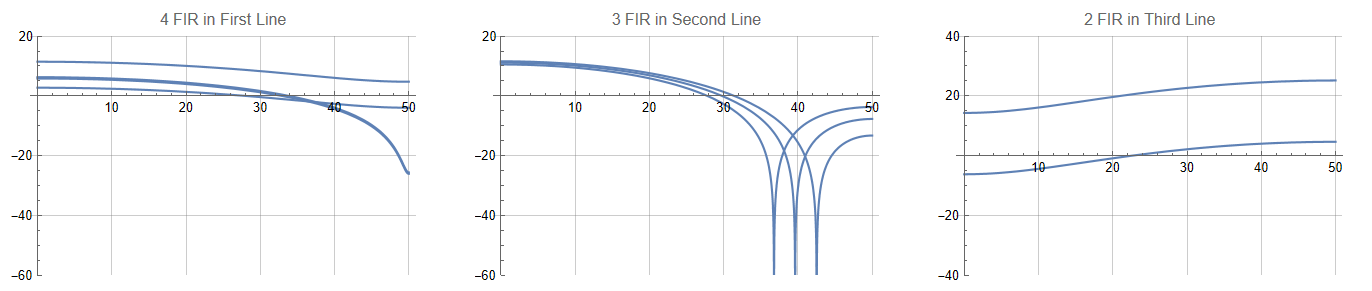
我们将这里的4+3+2这5个FIR分别求出他们的频响应,可以得到
ClearAll["Global`*"]
fs = 100;
z = Exp[2*I*Pi*f/fs];
h[1] = z + 2.7216413424166266;
h[2] = z + 1.052226182163558;
h[3] = z + 0.9503660115556205;
h[4] = z + 0.36742534161833024;
h[5] = z^2 + z*1.783419892212514 + 1;
h[6] = z^2 + z*1.5898117683847952 + 1;
h[7] = z^2 + z*1.3488814128927789 + 1;
h[8] = z^2 - 0.6066846548973727*z + 0.09414542532099852;
h[9] = z^2 - 6.4441225139598535*z + 10.621865019892331;
h1 = Plot[Table[20*Log10[Abs[h[i]]], {i, 1, 4}], {f, 0, fs/2},
MaxRecursion -> 15, GridLines -> Automatic, PlotRange -> {-60, 20},
PlotLabel -> "4 FIR in First Line"];
h2 = Plot[Table[20*Log10[Abs[h[i]]], {i, 5, 7}], {f, 0, fs/2},
MaxRecursion -> 15, GridLines -> Automatic, PlotRange -> {-60, 20},
PlotLabel -> "3 FIR in Second Line"];
h3 = Plot[Table[20*Log10[Abs[h[i]]], {i, 8, 9}], {f, 0, fs/2},
MaxRecursion -> 15, GridLines -> Automatic, PlotRange -> {-40, 40},
PlotLabel -> "2 FIR in Third Line"];
GraphicsRow[{h1, h2, h3}, ImageSize -> Full]
¶ 推导二阶传函零点
对如下 3-Tap 的传递函数(也就是有一对共轭复根的情况),代入
得到如下表达式,当然我们最终的目的是求出 和 与 (NULL 频点) 的关系,
为了在特定的归一化角频率 得到 Null 值,需要让虚部和实部都等于零。所以有
这样可以得到
将(5)代入到表达式(2),得到
当 Notch 点在原点的时候,此时是相同的两个一阶 FIR的级联
当 Notch 点在 或者 的时候,此时是相同的两个一阶 FIR的级联
¶ 50Hz抑制设计实例
输入 FIR 的 Input Data Rate 为 600Hz,输出的频率为 20Hz ,降采样率为 30,这样我们可以做一个长度为 30 的 FIR,这样就可以避免卷积运算,逐个相乘,每30次乘法后得到一次输出,理论上只需要一个乘法器依次相乘即可;
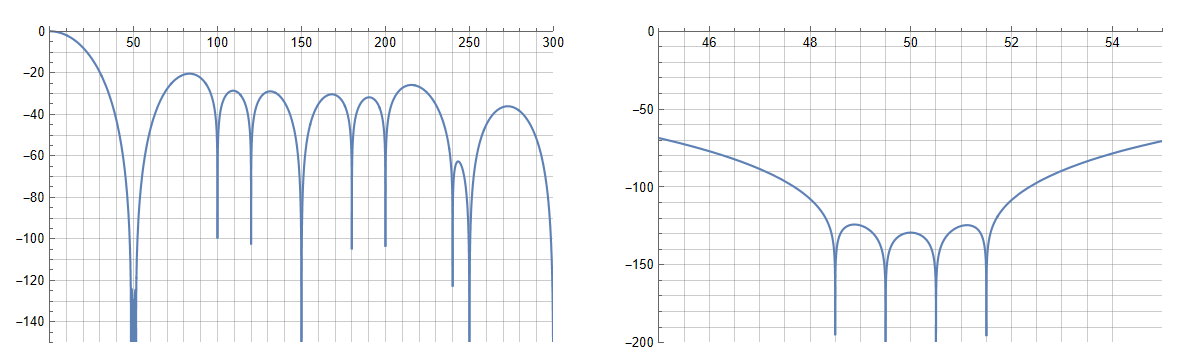
- zfm,首先放置3个Notch点在 fs/2,获得一定的低通特性;
- zf1,接着在 50Hz 附近 48.5 49.5 50.5 51.5 放置 Notch 点弥补 CLOCK 的偏移;
- zf2,接着在 fs/2 以内的 50Hz 的谐波处放置 Notch 点,100 150 200 250
- zfe,额外的抑制,150 250,在 fs/4 这个位置,放置一些 Notch 点,可以尽可能地实现低通的快速滚降低
- 混叠频率的考虑:这里 600Hz 的 Input Data Rate 很有意思,带内频率是 -300Hz to +300Hz,那么带外的 350-600=-250 恰好是带内的5次谐波的位置;有一种更巧妙的方式,比如 Input Data Rate = 220,放置完 50 60 100 三个 Notch 点后,120 - 220 = -100,60Hz 的二次谐波敲好落在了带内的100H处,更加节省
- 一阶 Filter 用了 3 个,二阶 Filter 用了 13 个,所以最后的响应长度长度为 3×1 (first-order) + 13×2 (second-order) + 1(zero-order) = 30
ClearAll["Global`*"]
zeroCoef[zf_, fs_] :=
List[1, -2*Cos[2*\[Pi]*zf/fs], 1]/(2 - 2*Cos[2*\[Pi]*zf/fs]);
fs = 600;
zfm = 3;
zf1 = List[48.5, 49.5, 50.5, 51.5];
zf2 = List[100, 120, 150, 180, 200, 240, 250 ];
zfe = List[ 150, 250];
b = 1;
For[m = 1, m <= zfm, m++,
{bz = FromDigits[List[1, 1]/2, z^-1]; b = b*bz;}]
For[m = 1, m <= Length[zf1], m++,
{bz = FromDigits[zeroCoef[zf1[[m]], fs], z^-1]; b = b*bz;}]
For[m = 1, m <= Length[zf2], m++,
{bz = FromDigits[zeroCoef[zf2[[m]], fs], z^-1]; b = b*bz;}]
For[m = 1, m <= Length[zfe], m++,
{bz = FromDigits[zeroCoef[zfe[[m]], fs], z^-1]; b = b*bz;}]
b = N[b // ExpandAll, 8];
fir = b /. z -> E^-(2*\[Pi]*I*f/fs);
xGrid = Table[i, {i, 0, 300, 10}];
yGrid = Table[i, {i, 0, -200, -10}];
p1 = Plot[20*Log10[Abs[fir]], {f, 0, 300},
GridLines -> {xGrid, yGrid}, PlotRange -> { {0, 300}, {-150, 0} },
MaxRecursion -> 12];
xGrid = Table[i, {i, 45, 54, 0.5}];
yGrid = Table[i, {i, 0, -200, -10}];
p2 = Plot[20*Log10[Abs[fir]], {f, 45, 55},
GridLines -> {xGrid, yGrid}, PlotRange -> { {45, 55}, {-200, 0} },
MaxRecursion -> 12];
GraphicsRow[{p1, p2}, Spacings -> 30]
¶ 参考资料
https://www.ednasia.com/synthesize-your-fir-filters-using-high-school-algebra/