¶ 1. 专利信息
根据截图中的文本内容(如“Field of the Invention”以及特定的现有技术引用),该技术对应的专利是 ADI 公司在 Sigma-Delta 领域非常著名的基础专利。
- 专利文件: US5404142_Butterfly_DEM.pdf
- 专利名称:Data-directed scrambler for multi-bit noise shaping D/A converters
- 发明人:Robert W. Adams (Bob Adams)
- 申请机构:Analog Devices, Inc.
该专利提出的核心动机是为了解决多位 DAC 中单位元失配导致的非线性问题。早期的解决方案如随机置乱(Random Scrambling)只能将谐波失真转化为白噪声,提高了底噪;而该发明通过引入“数据导向”的闭环控制,实现了对失配误差的噪声整形。
¶ 2. 二状态(2-State)积分控制
这是该专利提出的基础实施例。其核心思想是将整个置乱网络分解为若干个基本的“交换单元(Swapper Cell)”。每个单元接收两个输入位,并根据内部逻辑决定是“直通”还是“交叉交换”输出。
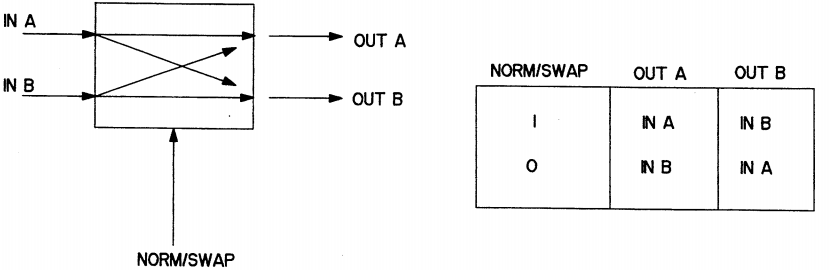
控制逻辑基于一个核心原则:误差的积分必须有界。每个交换单元内部维持一个状态变量,该变量代表了历史输出中,上下两个路径输出“1”的累积差值(Integration of Difference)。
在二状态机制中,积分差值被严格限制在 0 和 1 两个状态之间。逻辑电路监测当前的两个输入位以及当前存储的差值状态。当两个输入位不同(即一个为0,一个为1)时,逻辑电路会强制选择交换或不交换,以使得新的累积差值趋向于平衡。例如,如果上路历史输出的“1”比下路多(状态为1),且当前输入允许纠正,电路就会强制将当前的“1”导向下路,从而将差值状态清零。
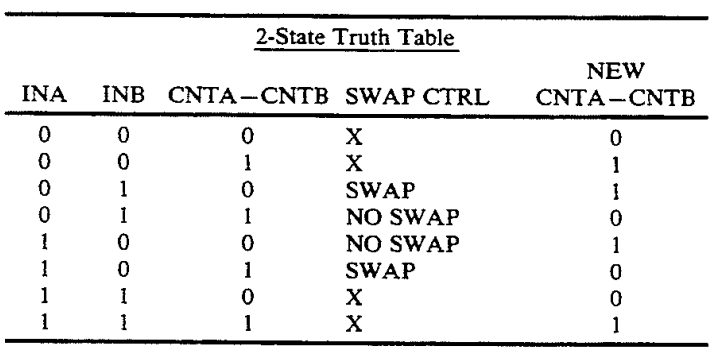
这种设计的精妙之处在于硬件实现的极简性。虽然理论上需要积分计数器,但由于状态被限制在 1-bit(0 或 1),实际电路只需要简单的组合逻辑(如异或门 XOR)和一个 D 触发器即可实现,无需复杂的加法器或多位寄存器。
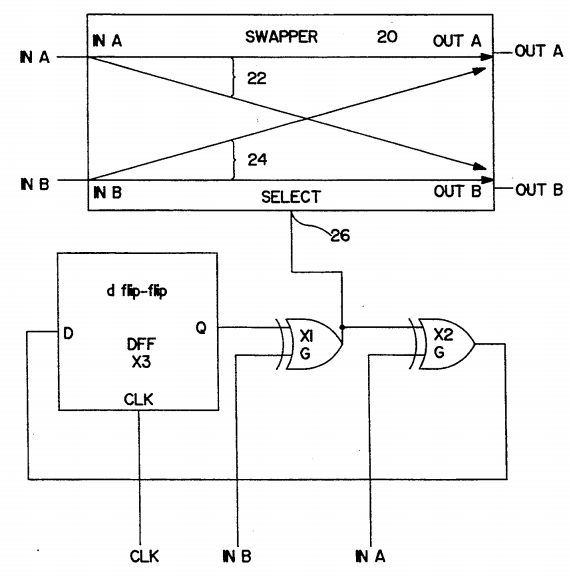
整体的 Butterfly 拓扑,以 8 Level 为例,有如下两种实现方式
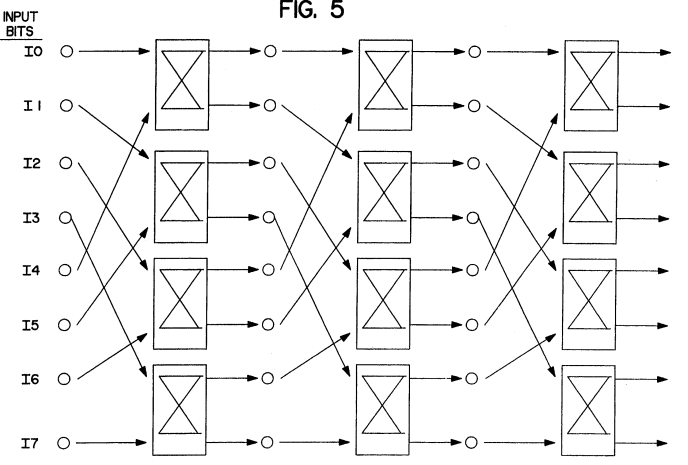
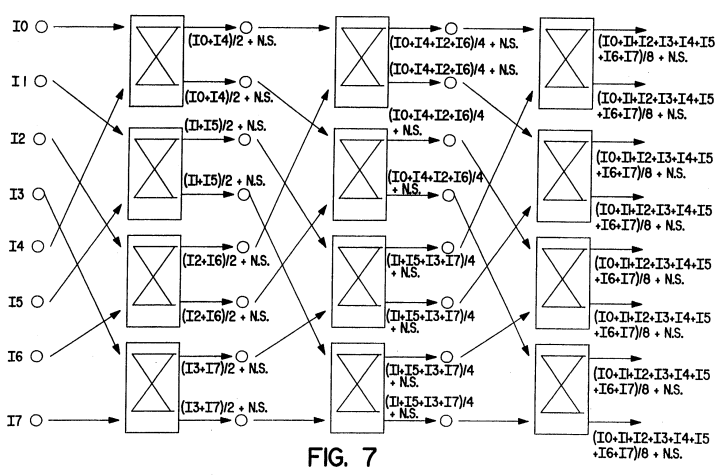
¶ 3. 三状态(3-State)与抖动引入
二状态机制虽然硬件简单,但由于其行为是完全确定性的(Deterministic),在某些特定的输入模式下容易形成固定的重复周期。这种周期性在频域上表现为“空闲音(Idle Tones)”或“模式噪声(Pattern Noise)”,即在频谱底噪上出现明显的尖峰,这对于高保真音频应用是不可接受的。
为了解决这个问题,专利提出了三状态改进方案。在这种模式下,允许积分差值在 -1、0、+1 三个状态中变化。增加的状态提供了一个“自由度”。
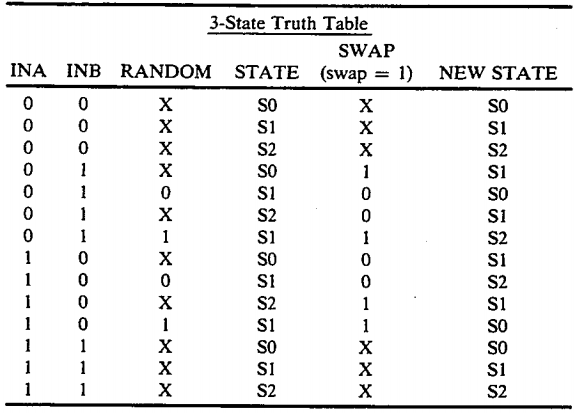
当积分差值为 0(即历史误差已完全平衡)且当前输入为不同值(0和1)时,系统处于“既不需要强制向上修正,也不需要强制向下修正”的中性状态。此时,控制逻辑引入一个随机位(Random Bit)来决定是交换还是不交换。这种随机性的引入打破了数据相关的周期性模式,有效地将离散的 Tone 能量打散并平铺到频谱中,起到了类似于 Dither(抖动)的作用,从而显著改善了 SFDR(无杂散动态范围)。
¶ 4. 噪声整形阶数的理论推导
该 Butterfly DEM 实现的是一阶(1st-order)失配误差整形。虽然文档中提到了“N阶”,但请注意原文的描述:“All of the scrambled output bits... is equal to the noise-shaping input plus an Nth-order noise-shaping term”。这句话是指:经过 DEM 后的总输出,依然保留了前端 Sigma-Delta 调制器本身的 N 阶量化噪声特性(例如 2 阶或 3 阶调制器)。DEM 没有破坏原有的量化噪声整形。对于 DAC 单元失配(Mismatch)引入的误差,原文明确指出:“Each individual output bit represents... plus a first-order noise-shaping term”。
该结构中的“交换单元”本质上是一个闭环反馈系统。控制信号是由历史输出差值的“积分”决定的。在信号处理中,如果一个误差信号(这里是失配误差)被积分后用于负反馈控制,那么其闭环传递函数将包含一个微分项(即积分的逆运算)。 在 Z 域中,积分器对应 。当它位于反馈路径时,误差传递函数(NTF)会呈现出 的形式,这正是典型的一阶高通滤波器的特性。因此,低频段的失配误差被抑制,并被推挤到了高频段。
虽然 DWA(数据加权平均)也是一阶整形,但 Butterfly 结构的优势在于它是分布式的,每个单元独立进行一阶整形,最终效果在统计上可能比简单的环形 DWA 更具鲁棒性,但数学本质上依然是一阶。
¶ 5. 优缺点深度分析与 DWA 的演进
既然 Butterfly 结构看起来逻辑严密且能实现整形,为什么现代高速 ADC/DAC 设计中 DWA(及其变种)占据了主导地位?以下是基于 IC 设计视角的深度分析:
缺点一:关键路径延迟(Latency)与级联效应 这是 Butterfly 结构在高速应用中的最大死穴。Butterfly 网络是分层级的(层数为 log2K)。请注意专利中的描述是“数据导向(Data-Directed)”。这意味着,第一级交换单元的状态决定了信号去往第二级的哪个位置;第二级的输入依赖于第一级的输出。 在电路实现上,这意味着数据必须像波纹一样穿过整个开关网络。对于一个 5-bit(32单元)的系统,信号需要连续穿过 5 层逻辑门和开关。在几百 MHz 甚至 GHz 的采样率下,这种级联的组合逻辑延迟(Propagation Delay)极易成为时序瓶颈,导致建立时间不足。相比之下,DWA 的逻辑可以并行化(通过桶形移位器和并行加法器),速度更快。
缺点二:硬件复杂度与面积 Butterfly 结构需要的开关单元数量是 N×log2N 级别的(或者更准确地说是 K/2×log2K)。对于 5-bit (32单元) DAC,虽然比全矩阵开关少,但依然需要大量的异或门和触发器分布在信号路径上。 更重要的是布线复杂度。Butterfly 的拓扑结构在版图(Layout)上意味着大量的交叉连线,这在拥挤的模拟版图设计中会引入寄生电容,可能引发串扰或进一步拖慢速度。
缺点三:Tone 的残留 即便是使用了 3-state 引入随机性,Butterfly 结构本质上还是基于“局部决策”的。每个单元只管自己的一亩三分地(即只平衡流经自己的那两个信号)。这种局部的平衡并不总是能保证全局的最佳平衡。 相比之下,DWA 是一种“全局旋转”策略,它强制所有单元在尽可能短的周期内被轮询一遍。在处理某些特定的直流或低频输入时,DWA 消除 Tone 的效果通常比 2-state Butterfly 更好且更可预测。虽然 3-state Butterfly 解决了这个问题,但它增加的硬件开销使得性价比不如改进型的 DWA(如 Bi-DWA 或 Partitioned DWA)。
缺点四:数量限制 Butterfly 结构基于 FFT 类似的基-2 算法,这天然要求单位元的数量 K 必须是 2 的幂次方(4, 8, 16, 32...)。然而在实际工程中,为了优化量化器设计或出于稳定性考虑,有时会设计非 2 幂次方的电平数(例如 1.5 bit 或其他奇数电平),DWA 可以通过简单的指针回绕逻辑适应任意数量的单元,而 Butterfly 结构则很难适配。
综上所述,Bob Adams 的这项 Butterfly DEM 专利是该领域的开山之作,它首次精妙地将数字信号处理中的流图概念引入模拟电路的失配校正,确立了“失配整形”的理论基础。但在随后的几十年中,随着采样速率的指数级提升,更适合高速并行处理且全局控制力更强的 DWA 算法逐渐成为了主流选择。