JSSC,2015,An Embedded 65 nm CMOS Remote Temperature Sensor With Digital Beta Correction and Series Resistance Cancellation Achieving an Inaccuracy of 0.4°C (3σ) From -40°C to 130°C
分立的BJT,或者嵌入到CPU/MCU芯片的寄生三极管,作为温度传感器的信号源。
主要挑战是
1,寄生二极管的β非常低,甚至低于1;且β随Emiter电流变化很大
2,串联电阻的影响;
当PNP BJT是二极管接法时,我们控制N倍比例电流是IE而不是IC
ΔVBE=qkT⋅ln(IC2IC1)=qkT⋅ln(IE2⋅β2/(β2+1)IE1⋅β1/(β1+1))
所以,最终的结果是
ΔVBE=qkT⋅ln(β2⋅(β1+1)β1⋅(β2+1)⋅N)
所以温度的表达式如下,注意将BETA分别表示,这样有助于之后BETA测量后的校准计算
T=ΔVBEln(N)(1−ln(N)ln(1+1/β2)+ln(N)ln(1+1/β1))q
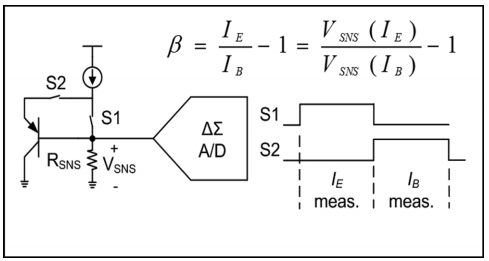
测试方法
- 将本来注入到Emiter的电流先注入到Rsens上,利用Rsens IE→V1,测出IE;
- 然后将电流注入到Emiter上,这样IB电流也回注入到电阻上,再次利用Rsens IB→V2,测出IB;
- 这样,Beta可以通过两次电压求出
β=IBIE−IB=V2V1−V2
如果在二极管连接的BJT上,分别用1:N的电流测得的电压得到Delta VBE,由于串联电阻的影响,实际测回的电压差为:
ΔV=ΔVBE+(N−1)IBIASR
那么单位电阻上噪声的误差为(°C/Ω):
ReR=qkln(n)(N−1)IBIAS
思想似乎是一个专利,US7541444B2,2024-6-20 Expiration
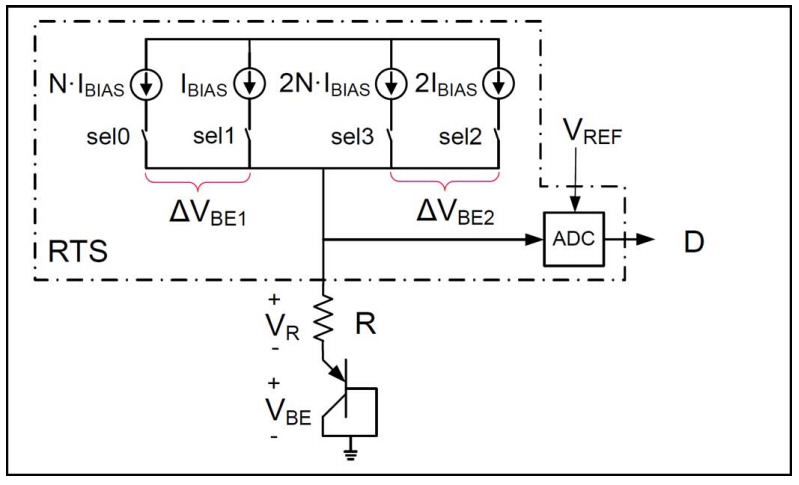
每次采样/积分过程是一个CDS,过采样下的积分又是多次求和的过程,一次正着积分采样,一次负着积分采样,又能做一次CDS,这样相当于做了两次的CDS,具体如下:
-
第一个采样-积分周期,2倍采样电容,采样相位时注入电流NI,积分相位时注入电流I,得到的积分电压
V1=2[qkTln(ISI)+I⋅R]−2[qkTln(ISN⋅I)+N⋅I⋅R]
-
第二个采样-积分周期,1倍采样电容,采样相位时注入电流2I,积分相位时注入电流2NI,得到的信号电压
V2=[qkTln(ISN⋅2I)+N⋅2I⋅R]−[qkTln(IS2I)+2I⋅R]
-
最终的电压为
V1=2VTln(N)+2IR−2NIRV2=−VTln(N)+2NIR−2IRV1+V2=VTln(N)

