¶ PLL Modules
PD (Phase Detect),最简单由一个XOR模块实现;
- 两个时钟异或之后会产生 Pulse,Pulse的均值电压反应了相位差
- 为了得到这个均值,PD 后面要跟一个 LPF,就是为了获得这个均值电压
- 不单调:相位差0180°,输出平均电压上升,负反馈;180°C360°C,输出电压下降,正反馈;影响锁定时间
PFD (Phase),Tri-State PFD
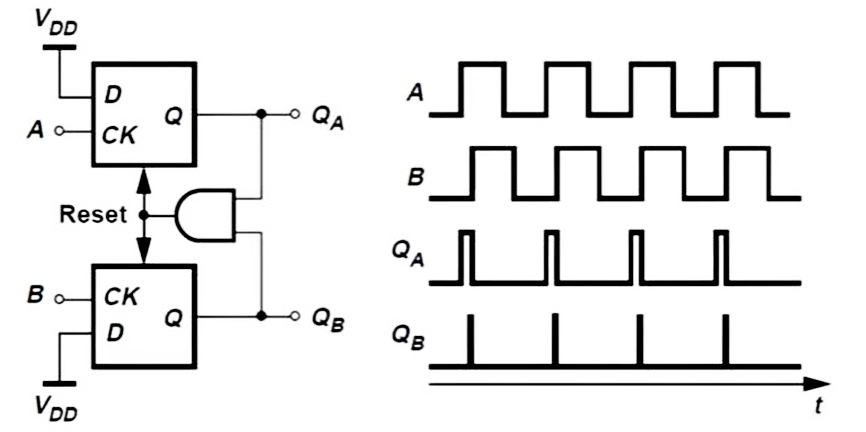
- RESET是高电平触发,QA-QB是输出,
- 输入相位差可以为
- 其正负相差的输出不对称,超出线性的 区间后。虽然 PFD的输入不能正确反映真实的相位差,但是负相位时输出永远为负,正相位时输出永远为正,这样就实现了对频率的 Detect,频率慢了以后,反馈总是趋向于让相位减小;频率快了以后,反馈总是让相位增加;这样输入和基准的初始状态就没有影响了。
Tri-State-PFD 后会跟一个 Charge Pump + PD,用于实现积分器,
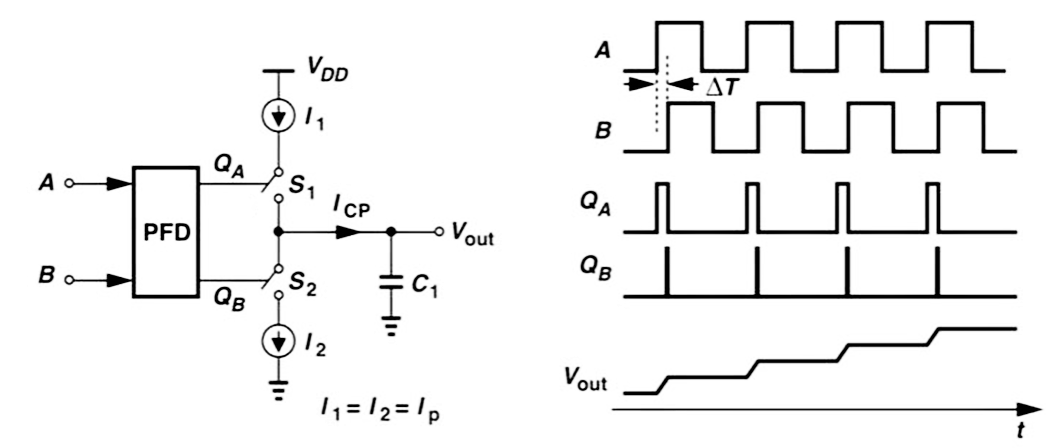
- PFD+CP 的增益是
- 积分器用于实现在原点的极点
- 电流的积分会比电压积分容易很多,用为不需要用 OPA(其实用OPA,实现电压的积分,也是利用OPA和电阻电容,将 Voltage 转换为 Current 完成积分后再转换为 Voltage,所以直接用电荷泵就可以了)
- 滤波器,C或者RC的组合,增加R的目的是稳定性考虑,作用是为了提取 PFD+CP 输出的平均值,所以需要有低通特性
- 不使用有源滤波器,是噪声的考虑
VCO 压控振荡器
- 输出频率频率 , 的单位是 ,这里的 其实是个小信号的 Δ 量
- 是 VCO 的直流分量,在小信号分析的时候,只对交流分量分析,所以 VCO 的表达式为
- 相位是频率的积分,于是相位变量
- 在 s 域,VCO 的传递函数为如下,因为积分的 Laplace 变换是
分频器
- 在环路中,实现倍频的效果
- 分频器的线性度非常重要,尤其是对小数分频的频率综合器(分频器会引入一个固定延迟,小数分频器总,分频比改变时,这个延迟不一样,高频噪声的折叠,以及杂散的产生)
- 对输出加入 re-timing 可改善线性度以及相位噪声
¶ PLL Linear Model and Type-I PLL
闭环传递函数为
对比经典的二阶系统的传递函数
利用自然频率和阻尼系数去设计,一般 是已知的
另一种方法,开环稳定性分析
¶ PLL Linear Model and Type-II PLL
TYPY-I PLL 的局限性
- 频率与相位差成正比,需要有相位差才能产生 V CONTROL
- 增加 KVCO 会导致稳定性有稳定性问题
TYPY-II PLL 的特性
- 没有相位差;
- LPF可以使用不同结构补偿稳定性/噪声控制,一阶C/一阶RC/二阶EC