A voltage-averaging feedback (VAF) concept is proposed to overcome conventional relaxation oscillator problems such as sensitivity to comparator delay, aging, and flicker noise of current sources.
- Reference: An On-Chip CMOS Relaxation Oscillator With Voltage Averaging Feedback
- JSSC 2010
- Frequency: 14MHz
- Process: 1.8V 0.18um Standard CMOS
- Power: 25uA
- Temperature Coefficient: ±0.19% for -40°C ~ 125°C
- Area: 0.04mm2
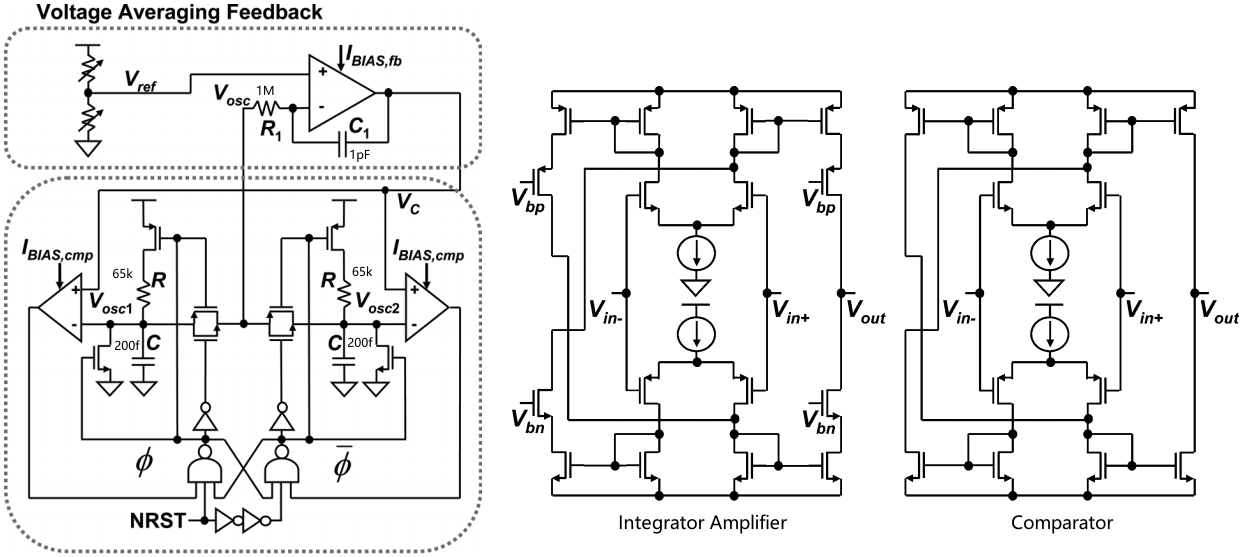
主要优势:使用R充电而非电流源可以较少电流镜的 flicker noise,与此同时R的匹配较好可以保证占空比;使用连续的积分器,同样可以避免采样混叠提高噪声功耗效率;积分器的 amplifier 内部没有高阻节点自然不需要补偿主极点在外部,实现了 folded cascode 的增益,几乎不关心线性度等参数所以也不需要做恒 gm 偏置等操作;
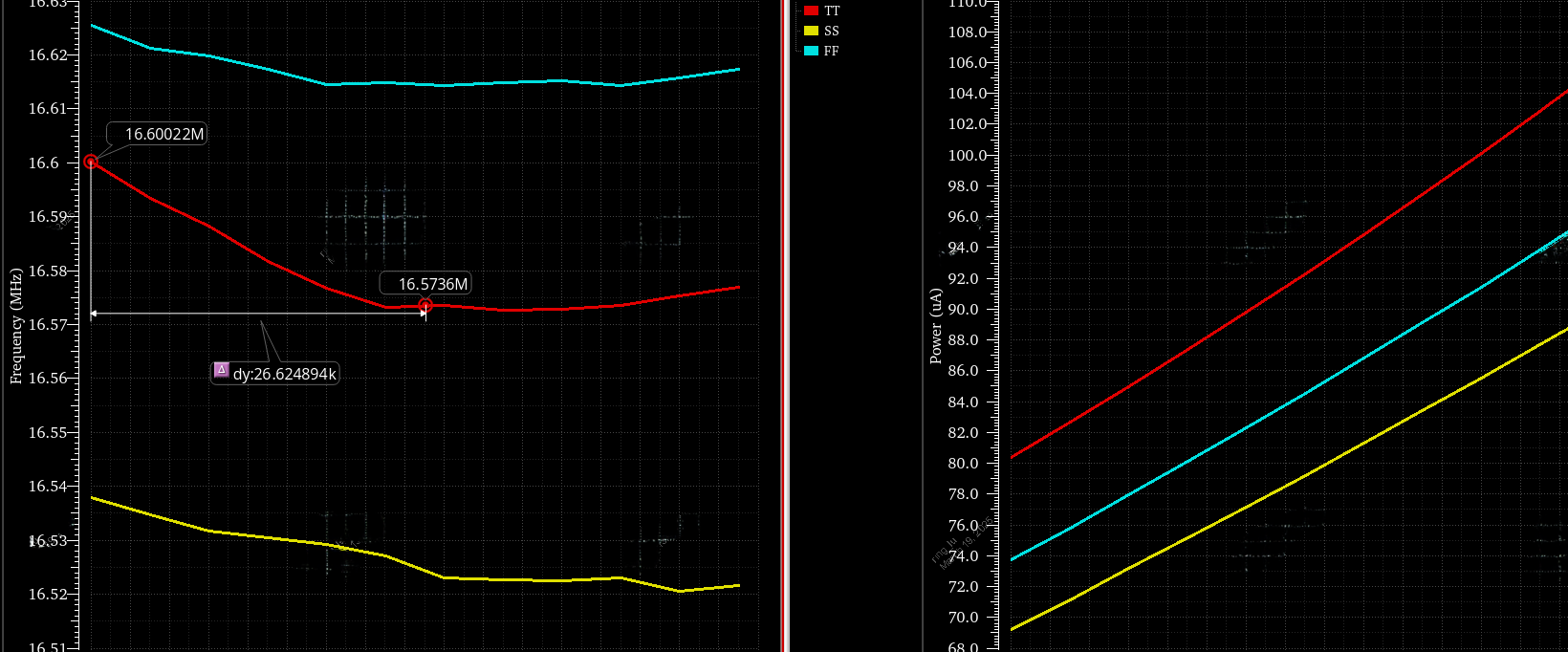
TSMC 0.18um BCD 工艺,初步搭建电路仿真结果,83uA -> 40uA(待优化),-40°C ~ 125° 频率最大变化0.16%,核心设计点如下:
- 使用 TFR = 33K, C=544f;
- 使用 ΔVgs/TFR 的PTAT 电流源对 OTA/Comparator 偏置
- Compartator的N/P偏置都是2.4uA,镜像复制都是 1:3
- OTA的N/P偏置都是1.5uA,镜像复制都是1:1
- tgate的开关的 charge injection 有较大影响,N/P 都选取了 0.35u/0.18u
求解积分器的传递函数,假设理想 OPA 的传递函数 Hopa(s)=1+s/τA
Vc(s)Vc(s)∣A→∞,τ→0=⎝⎜⎜⎜⎛Vref−⎝⎜⎜⎜⎛R1+sC11sC11Vosc1,2(s)+R1+sC11R1Vc(s)⎠⎟⎟⎟⎞⎠⎟⎟⎟⎞Hopa(s)=sR1C1Vref(1+sR1C1)−Vosc1,2(s)(1)
分析积分器的输出信号 Vc(s)
- 当信号频率 ω≪R1C11 时,Vc(s) 同时包含 Vref 和 Vosc1,2(s) 的贡献
- 当信号频率 ω≫R1C11 时,Vc(s) 就几乎只有 Vref 的成分了
我们估计 Vosc1,2(t) 信号,其最多是一个周期为 T=5RC 的周期信号。根据傅里叶变换的性质,时域周期则频域离散,对于周期信号,其频域只会出现在 nωo=5RC2πn,除了DC外,其频率成分都远高于积分器对 Vosc1,2(t) 的响应频率,nω0=5RC2π≫R1C11
所以,对于频域离散的 Vosc1,2(s) 能对环路控制有效果的只剩下了 0 rad/s 频点的信号了,所以只需要分析 Vc(0) 和 Vosc1,2(s) 的传递关系,假设比较器 + RC 充电的传函为 Hramp(s)=Vosc1,2(s)/Vc(s)
Vosc1,2(s)Vosc1,2(0)Vosc1,2(0)=sR1C1Vref(1+sR1C1)−Vosc1,2(s)Hramp(s)=Vref1+Hramp(0)0R1C11+0R1C1=Vref(2)
虽然传函Hramp(s)在严格意义上是求不出来的,RC Ramp 信号 Vosc1,2 上升到 Vc 时,系统复位,这是一个非线性时变系统,无法写出 s 域传递函数(Laplace Transformation 只支持线性时不变系统,非线性时变系统的准确特性需要通过 Cadence/Simulink 中进行 transient 瞬态仿真得到),但是我们只分析其DC特性,这样就是时不变系统了。
至于非线性,我们这里也没有对其进行非线性建模;且高增益的反馈是可以抑制 Gain Stage 后非线性误差的,所以这里我们不去关注它(即使需要分析,我们也可以利用级数工具)。
到此,我们知道了,由于积分器的存在,周期 Ramp 信号 Vosc1,2(t) 只有低频才能通过,使得线性化近似也不会引入不可接受的误差。对于周期信号,我们提取其 DC 信号,只需要对一个周期,求解傅里叶级数中的第 0 项即可,即
XnVosc1,2(0)=T1∫0TVosc1,2(t)e−jnω0tdt=T1∫0TVosc1,2(t)dt(3)
接着,我们代入 Vosc1,2(t) 的表达式
⎩⎪⎪⎪⎨⎪⎪⎪⎧Vosc1,2(t)=Vdd(1−e−t/(RC))α=VddVref(4)
结合(2)(3)(4)将会得到如下方程,求解节分后得到周期 T,RC,α 的关系
VrefVddVrefααTαTRC(1−α)T=T1∫0TVdd(1−e−t/(RC))dt=T1∫0T(1−e−t/(RC))dt=T1∫0T(1−e−t/(RC))dt=t+RCe−t/(RC)∣∣∣∣∣0T=(T+RCe−T/(RC))−(0+RC)=1−e−T/(RC)(5)
to be done
Vc(s) 的时域为
Vc(t)=L−1{Vc(s)}=R1C1Vrefu(t)+Vrefδ(t)−L−1{sR1C1Vosc1,2(s)}
s 域乘积意味着时域做卷积,所有接着
Vc(t)=R1C1Vrefu(t)+Vrefδ(t)−R1C1Vosc1,2(t)∗u(t)=R1C1Vrefu(t)+Vrefδ(t)−R1C11∫0tVosc1,2(τ)u(t−τ)dτ=R1C1Vrefu(t)+Vrefδ(t)−R1C11∫0tVosc1,2(τ)u(t−τ)dτ
因为用了单边 Laplace 变换,所以产生了 u(t);但是我们研究的是真实的物理系统,所以 u(t−τ)=1 的,所以可以接着简化为
Vc(t)=R1C1Vref+Vrefδ(t)−R1C11∫0tVosc1,2(τ)dτ
压控 RC Ramp,要在某个 t′ 时刻,让 Vosc1,2(t) 充到 Vc(t);这里的 t’ 时刻也就是一半的振荡器周期,因为两个充电周期完全一致,我们就研究一半的周期即可;所以有如下关系
Vosc1,2(t)Vosc1,2(T)Vosc1,2(T)=Vc(t)=R1C1Vref+Vrefδ(T)−R1C11∫0TVosc1,2(τ)dτ=R1C1Vref−R1C11∫0TVosc1,2(τ)dτ
压控 RC Ramp 的时域如下
⎩⎪⎪⎨⎪⎪⎧Vosc1,2(t)=Vdd(1−e−t/(RC))Vosc1,2(T)=Vc(T)
如果定义 α=Vref/Vdd
⎩⎪⎪⎨⎪⎪⎧Vosc1,2(t)=Vdd(1−e−t/(RC))Vosc1,2(T)=Vc(T)

