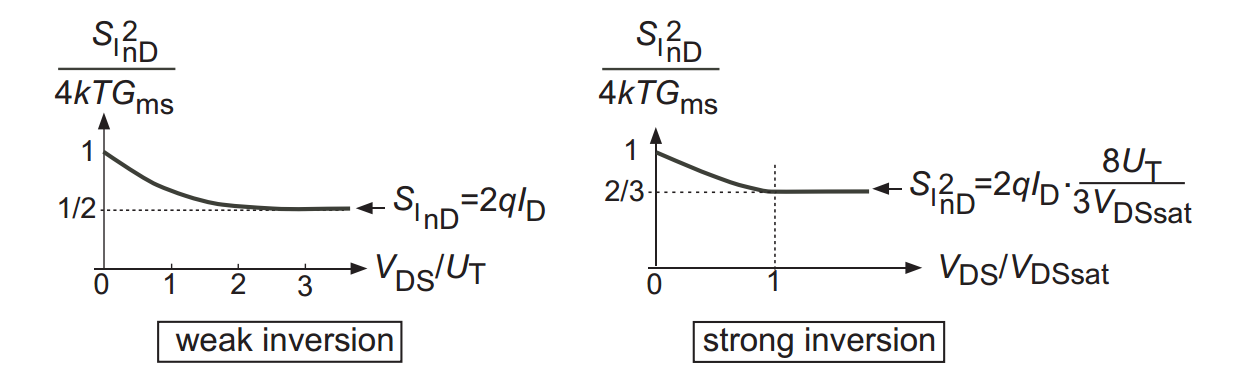电流用 Forward 电流和 Reverse 电流表示,分别被 VSG 和 VDG 两个电压控制
ID=I(VS,VG)−I(VD,VG)=IF−IR(1)
这里的正/反向电流的表达式为
IF(R)Ispec=Ispec[ln(1+exp2nUTVG−VT0−nVS(D))]2=2nμCoxLWUT2(2)
- VT0 是当 VS=0 时的阈值电压;
- n 是 slop factor, value ranging from 1.1 to 1.6
- UT=kT/q ,温度相关的一个 thermodynamic voltage, 26mV at 27°C
- μ 是载流子载流子迁移率 mobility
- Cox 是单位面积的栅电容
- W/L 是器件沟道的宽长比
如果 IF(R)≪Ispec ,transistor 工作在弱反型区 weak inversion;此时表达式简化为
IF(R)Ispec=IspecexpnUTVG−VT0−nVS(D)=2nμCoxLWUT2(3)
如果 IF(R)≫Ispec ,transistor 工作在强反型区 strong inversion
IF(R)Ispecβ=Ispec(2nUTVG−VT0−nVS(D))2=2nβ(VG−VT0−nVS(D))2=2nμCoxLWUT2=μCoxW/L(4)
饱和区 IR≪IF,也就是 Drain Current 远小于 Source Current,似乎 ID 与 Drain 电压关系不大,此时工作在饱和区; Inversion Coefficient以下公式表示
IC=max(IspecIF,IspecIR)(5)
跨导 Gm 通过对公式(2)分别对 Vs(d) 求导,得到
Gms(d)=−dVs(d)dIF(R)=UTIF(R)Ispec(1−eIF(R)/Ispec)(6)
如果是正向饱和,即 IF≫IR,Gms≫Gmd,公式(2)对VG求导,可以得到
G_m=\frac{G_{ms} }{n}=\frac{\sqrt{I_DI_{spec} } }{nU_T}\left(1-e^\sqrt{I_D/I_{spec} }\right)=\frac{I_D}{nU_T}\cdot\frac{1-\sqrt{IC} }{\sqrt{IC} }\tag{7}
Gms(d)Gm=UTIF(R)=n1(UTIF−UTIR)=nUTID (weak inversion)(8)
在强反型区,\left(1-e^\sqrt{I_D/I_{spec} }\right)\rightarrow 1,所以可以简化公式(7)为
Gm=nGms=nUTIDIspec=nUTICID(9)
同时在强反型区,通过对公式(4)求导,可以得到
Gm=n2βID=nβ(VG−VT0−nVs)(10)
Drain 端的 Gds 为,VM 是 Channel Length Modulation Voltage
Gds=VMID(11)
这里的 VM 正比于 Channel Length L,接着代入一般的公式(7),可以得到本增增益
AV0=GdsGm=nUTVM⋅IC1−e−IC(12)
如果 VD=VS,也就是在线性区
SInD2=4kTGms(13)
如果工作在饱和区,则有如下表达式
SInD2=4kTγtGms=4kTγtnGm(14)
这里弱反型区 γt=1/2,强反型区 γt=2/3,短沟道期间这些参数会更大
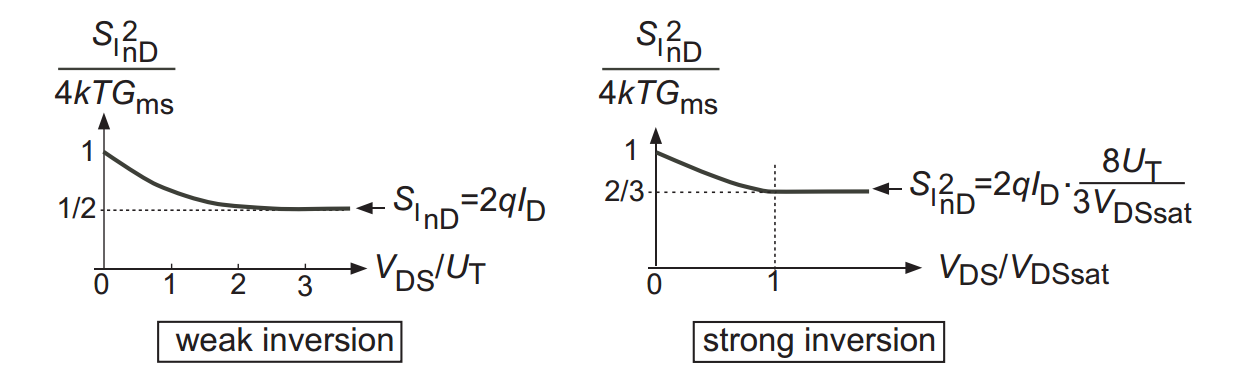
观察上图,注意这里的跨导是 Gms 对 VS 的而不是对 VG 的,而且仅仅是白噪声的部分。管子工作在弱反型区,噪声更多是散粒噪声 shot noise,散粒噪声仍然是一种白噪声。
- 散粒噪声是由于电荷的离散性引起的。在晶体管中,电流是由离散的电荷载流子(如电子或空穴)传输的,这些载流子的流动是随机的,导致电流的波动。
- 散粒噪声主要出现在直流电流中,尤其是在二极管或晶体管的正向偏置区域(如饱和区或弱反型区)。
SIn,shot2=2qID(15)
这里的 q=1.6×10−19 是基本电荷
Flicker Noise 基本呈现出以下形式,只是轻微地在 medium inversion 中略小,weak/strong inversion 中略大的特点
SVnG2=ωnKf, where Kf∝WL1(16)