¶ LFSR 介绍
LFSR,全程 Linear Feedback Shift Register(线性反馈移位寄存器),用于产生 Pseudo-Random Sequence (伪随机序列),这里介绍基于 XILINUX XAPP052 这个应用手册中产生最大长度的随机序列方法。
参考资料下载:xapp052.pdf
LFSR 由两个核心部分组成:
- 移位寄存器(Shift Register): 一串级联的触发器,每个时钟周期将数据向右或向左移动一位。
- 反馈函数(Feedback Function): 通常由某些特定位置(称为 抽头/Taps)的位通过异或(XOR)或同或(XNOR)运算后,反馈回寄存器的输入端。
关键概念
- 特征多项式(Characteristic Polynomial): 描述抽头位置的数学表达式,例如 。
- 状态周期: 如果多项式是本原多项式(Primitive Polynomial),一个 位的 LFSR 能产生长度为 的最大长度序列(M-序列)。
- 全零陷阱: 在使用 XOR 反馈的情况下,寄存器不能处于全 0 状态,否则会陷入死循环(始终输出 0);如果使用 XNOR 反馈的情况下,寄存器不能处于全 1 状态
Notes: 背后的数学机理是 Primitive Polynomials,等之后由空闲了再去补充这部分内容
¶ 基本结构与任意周期
XILINX 的 XAPP052 这个应用手册,介绍了标准的 LFSR 序列产生方法,以 4 阶为例
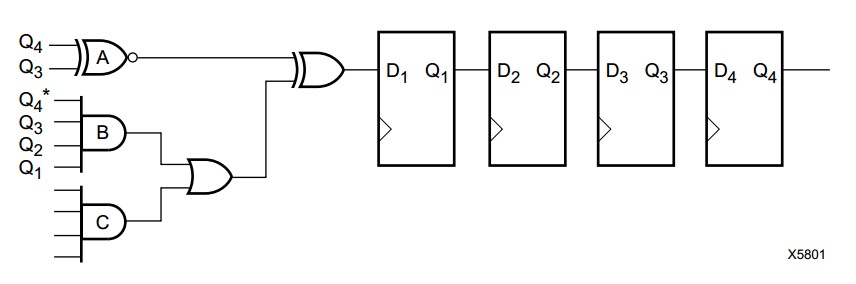
- A 门 XNOR,用于产生最大长度序列的反馈系数;如果这里使用的 XNOR,意味着全1是非法状态;如果这里使用的是 NOR,意味着全0是非法状态。一个标准的 LFSR,可以仅由 n×DFF + XNOR 构成,不需要其它逻辑门。
- B 门 AND 用于将本来非法的全 1111 状态,安全地塞回到这个序列中,这样本来 LFSR 只能产生 2^N-1 个状态序列,现在可以产生 2^N 个状态了;例如为了让 1111 也进入 Loop,B 门的 Q4 不接,使用 AND3 即可;
- C 门,这也是 XAPP052 这篇手册精华的部分,可以实现任意的周期
- 如果周期是15,那么 C 门不要,B门接入Q4,或者干脆什么都不要,这个的目的是移除异常的全 11111 非法状态
- 如果周期是2,那么 C 门接入 ,B 门都不要接入Q4
- 如果周期是3,那么 C 门接入 ,B 门都不要接入Q4
- 如果周期是4,那么 C 门接入 ,同时 B 门接入 Q4
- 如果周期是5,那么 C 门接入 或者 都可以,B 门都不要接入Q4
- ...
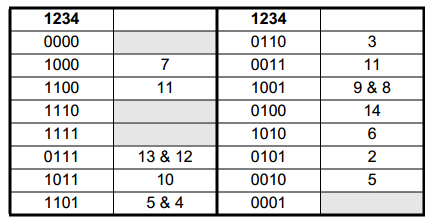
也就是说,这里的表中的第一列,是译码值用于填入 C 门的;第二列是周期数;涉及到 & 的,表示这里可以实现两种周期,B门的最高位Q4 不接入,那就实现 & 左侧的周期,B门的 Q4 接入,实现的就是 & 右边的
更进一步观察这个表格
- 其实左边这列就是这个 LFSR 产生的序列的顺序,复位到 0000 后,之后就是 1000 - 1100 1110 ... 这样一次进行;
- 如果在 1000 这里下次强制反馈 0 而非1,那么下一个状态就变成了 0100 而非 1100,这样就直接跳过了很多个状态,从而实现了周期为 7
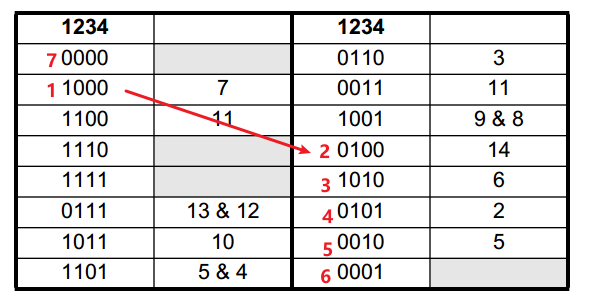
¶ 上至 168 bits XNOR 反馈
这里手册给出了 168 阶的 LFSR,为了实现最大长度的序列,XNOR 应该选哪个抽头,这个实现方式就是最经典的 LFSR 结构,只需要 n×DFF + XNOR 即可,这样就可以实现 2^N-1 个状态序列