这篇文章推推导了两种 Bandgap Core 的反馈系数。我们希望反馈系数 β 大,这样放大器的非理想特性(噪声/失调)在输出端的体现 Vnoise,offset/β 会尽可能减少。
基于寄生三极管做的 Bandgap,其 Collector 只能在衬底上,因此其有一端必须接到电源轨,例如寄生的 PNP 来看,其 Collector 只能是 PSUB,这样的 BJT 自身的 β 也比较小,通常只有 1~2,受基极电流的影响比较大。使用这种工艺设计 Bandgap 的结构也比较受限,典型结构如下
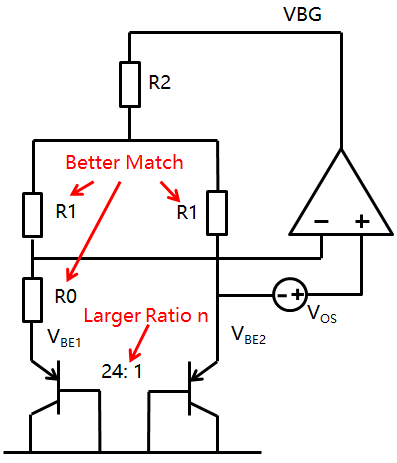
基本的BJT公式,以及 R1 和具有 VOS 的放大器构成电流镜像
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧VBE1VBE2IC2=VTln(nIsIC1)=VTln(IsIC2)=R1IC1R1+VOS=IC1+R1VOS
根据放大器输入端电压相等,可得如下关系
VTln(8IsIC1)+IC1R0IC1R0=VTln⎝⎜⎜⎜⎛IsR1IC1R1+VOS ⋅IC18Is⎠⎟⎟⎟⎞+VOS=VTln⎝⎜⎜⎜⎛IsR1IC1R1+VOS⎠⎟⎟⎟⎞+VOS=VTln(8)+VTln(1+IC1R1VOS)+VOS
求解得到 IC1
IC1=R0VTln(8)+R0VTln(1+IC1R1VOS)+R0VOS
从 VBE1 这条支路,逐渐相加,得到输出的 VBG 电压是
VBG = VBE1 + IC1(R0+R1+2R2) + (IC2−IC1)R2
代入 IC1,C2,可以得到最终的输出电压
VBG=VBE1+VTln(8)R0R0+R1+2R2+VTln(1+I1R1VOS)R0R0+R1+2R2+VOSR0R0+R1+2R2+VOSR1R2
同理,我们也可以从 VBE2 这条支路逐个叠加,得到输出的 VBG 电压是
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧IC2VBG =R0VTln(8)+R0VTln(1+I1R1VOS)+R0VOS+R1VOS= VBE2 + IC1(R1+2R2) + (IC2−IC1)(R1+R2)
VBG=VBE2+VTln(8)R0R1+2R2+VTln(1+I1R1VOS)R0R1+2R2+VOSR0R0+R1+2R2+VOSR1R2
直观分析大信号下 VBG 的表达式:两个 BJT 的比例 n 越大,为了电压温度持平,R0 就可以越大,此时反馈回输入电压越大。
在 BJT 小信号模型下,diode connected BJT 的阻抗仅与电流有关,用 rd 表示
rd=gm1=ICVT=r0VTln(n)VT=ln(n)r0
R2下面的电阻,可以看成是两个电阻的并联,用 rb 表示
rb=(rd+r0+r11+rd+r11)1=r0+2r1+2rd(r1+rd)(r0+r1+rd)
反馈路径
⎩⎪⎪⎪⎨⎪⎪⎪⎧βnβp=rb+r2rbrd+r0+r1r0+rd=rb+r2rbrd+r1rd
整体的反馈系数
β1=βn−βp1=log2[n]1r1r0+log[n]1r1r0+2(r1+r2)+r1r1+r2+r0r1+2r2
ClearAll["Global`*"]
r2=r2;r0=r0;n=n;
α=α;
r1=α*r0-2*r2;
rd=r0/Log[n];
rb=(rd+r0+r1)*(rd+r1)/(rd+r0+r1+rd+r1);
βn=rb/(rb+r2)*(r0+rd)/(rd+r0+r1);
βp=rb/(rb+r2)*rd/(rd+r1);
β=βn-βp;
a=FullSimplify[1/β,Assumptions->{r0,r2,n,α}∈Integers]
b=Collect[a, Log[n]]
这里,R2 仅仅是为了节省电阻而用的,其实完全可以合并到 R1 去,最终依靠 R1/R0 实现温度现数的抵消,因此有
β1=log2[n]1r1r0+log[n]1r1r0+r0r1+3
某种程度上,从大信号上来看,log[n]×(r1/r0) 是趋向于定值,这个从 VBG 的表达式简化掉 R2 可就以观察到,政府温度系数是需要抵消的
VBG=VBE1+VTln(8)R0R0+R1+VTln(1+I1R1VOS)R0R0+R1+VOSR0R0+R1
如果不使用寄生三极管,使用 BCD 工艺实现隔离井电位的话,就可以实现大名鼎鼎的 Browkaw 结构,如下所示
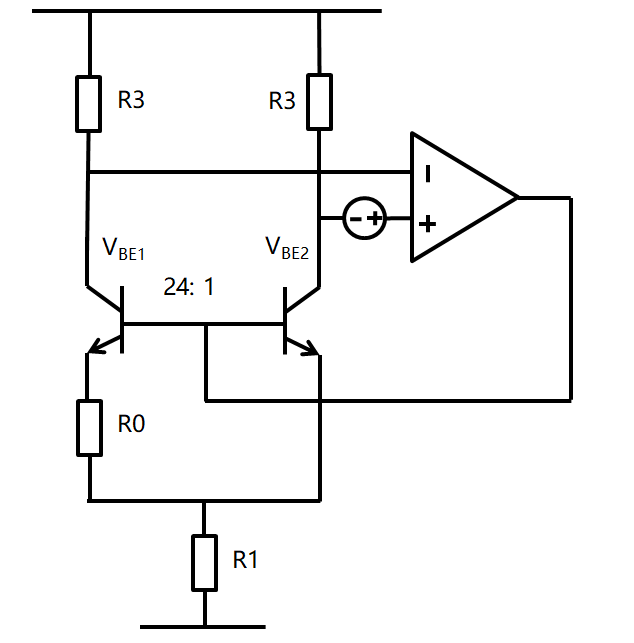
通过下面的推导,可以认时到这种结构虽然噪声小,但是VCE、VCB的电压变化很大,受厄利电压和的漏电影响大。论文认为是 Collector 端到Sub的漏电。
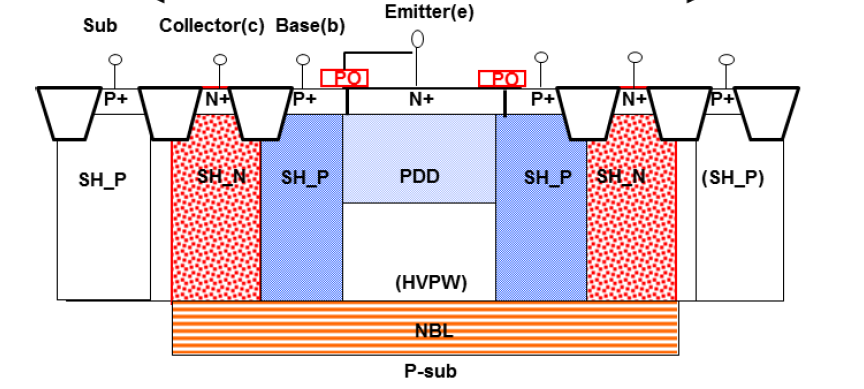
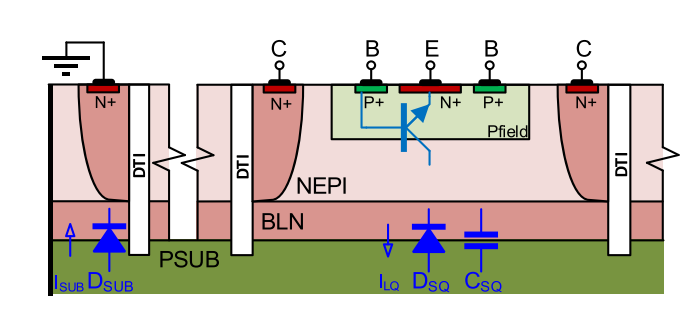
计算思路
- 先计算输入两条之路总的gmt对Vout产生的电流
- 计算电流的分流
- 计算左边之路电流在R0上产生的电压,其实也就是两个BJT的ΔV
- 将这个电压差转换为IC电流,然后乘以R3就是等效的反馈电压Vind
Vout⋅1+gmtR1gmt⋅gm1+gm2gm1⋅R0⋅gm⋅R3=Vind
βsystem=VoutVind=1+gmtR1gmt⋅gm1+gm2gm1⋅R0⋅gm1⋅R3
这里,gmt=gm1+gm2,注意gm=Ic/vbe,而gme=IE/vbe,这就需要考虑β对BJT的影响了。
gm1=1+gmeR0gme, gm2=gme, gme=(1+βBJT1)gm
代入得到
βsystem=β2+(β+1)gm(R0(β+(β+1)R1gm)+2βR1)β(β+1)R0R3gm2=gm(R0(R1gm+1)+2R1)+1R0R3gm2
ClearAll["Global`*"]
(*\[Beta]=2;
Subscript[g,m]=215*10^-6;
Subscript[R,3]=100*10^3;
Subscript[R,0]=10*10^3;
Subscript[R,1]=31.75*10^3;*)
Subscript[g, me] = Subscript[g, m]*(1 + 1/\[Beta]);
Subscript[g, m1] =
Subscript[g, me]/(1 + Subscript[g, me]*Subscript[R, 0]);
Subscript[g, m2] = Subscript[g, me];
Subscript[g, mt] = Subscript[g, m1] + Subscript[g, m2];
ans = Subscript[g, mt]/(1 + Subscript[g, mt]*Subscript[R, 1])*
Subscript[g, m1]/(Subscript[g, m1] + Subscript[g, m2])*
Subscript[R, 0]*Subscript[g, m]*Subscript[R, 3]
ans = FullSimplify[ans,
Assumptions -> {Subscript[g, m], Subscript[R, 3], Subscript[R, 0],
Subscript[R, 1], \[Beta]} > 0]
ans = Series[ans, \[Beta] -> Infinity]



