- Line Regulation (DC), PSRR (AC), Overshoot/Undershoot (tran),
- Load Regulation (DC)
- 瞬态,从尖峰到稳定(最终值的90%或更大)的时间称为恢复时间
负载电容的目的是为了让负载电流跳变时起到稳压作用
通过最大输出电流以及0.3V的最低VG,定出Power PMOS的尺寸,最后留出20%的Margin
EA+Power的结构中,EA用单级五管运放的输出摆幅受限,二级运放稳定性难搞,因此可以用第一级时diode-load的两级运放。
米勒补偿时,主极点不一定在里面
Capless LDO并非没有输出Decoupling电容,而是集成在内部。
假设等接受的电压波动为ΔV=10mV,ΔT=100ps的尖峰电流Ipeak=10Imax=100mA不能通过环路去响应,因此这部分电荷将完全由电容Cload来提供,那么有
21×Imax×ΔTCload=Cload×ΔV=21×Imax×ΔT/ΔV=5nF
几乎不能把主极点放在外面,因为片内电容很小。内部极点需要做的恒高,功耗会非常大;
使用单级放大器做EA+米勒补偿也不太现实,首先实现稳定,需要一定的静态输出级电流维持次级点位置。一旦想要提高GBW去改善瞬态overshoot就意味着要同时增大EA和输出级的速度,减小CC的方式去提高带宽不太现实是因为米勒电容要主导大过功率管的栅极电容。所以最终只有一条路可以走就是提高电流。
使用两级EA,让米勒电容跨接EA第二级+功率管的做法,可以提高一点功耗效率。一个的作用了让米勒电容不再被很大的功率管栅电容分压;这里的第二级最好是一个Buffer而非增益级,这样可以避免功率管栅级的次级点压力。
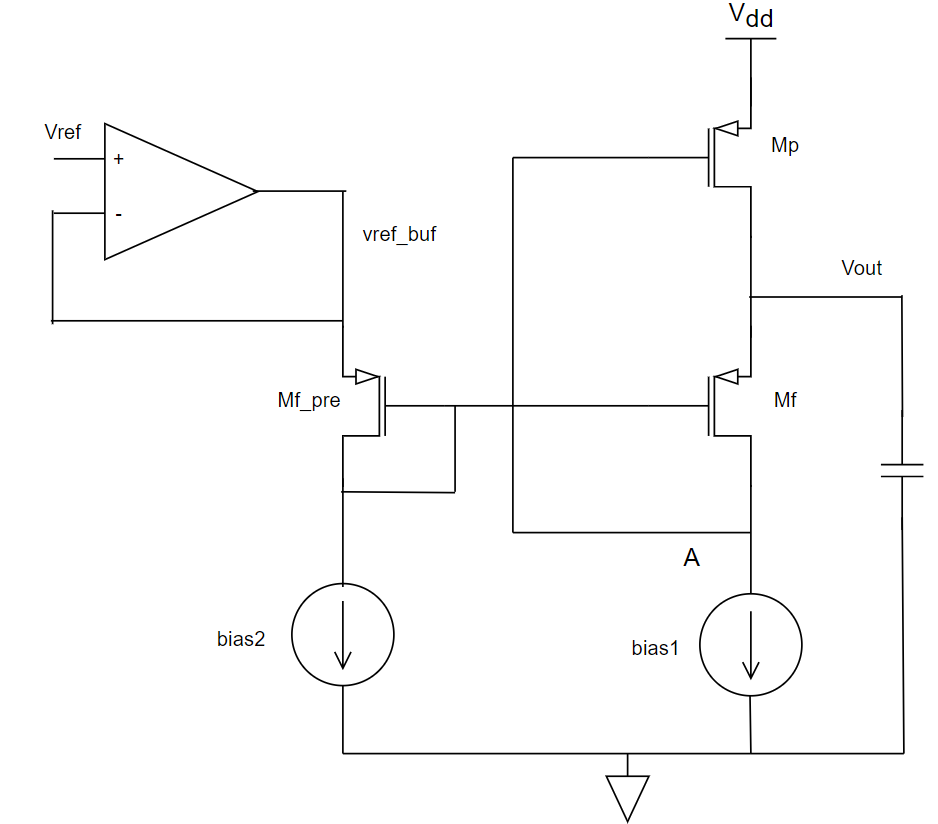
该结构的输出阻抗计算,直通的V→I的导纳,可以知道流入的电流是由两部分产生的,第一部分是下面的等效阻抗,这个通过MOSFET-Input-Output-Resistance的公式可以得到
Iin1=1+gmfRfRb+RfVout
另一部分电流,是一位因为Iin1在A点产生的电压后,通过MP流入的电流
Iin2=Iin1Rbgmp
所以总的电流是
Iin=Iin1+Iin2=1+gmfRfRb+RfVout(1+gmpRb)
最终输阻抗为
IinVout=1+gmfRf+gmpRb+gmfRfgmpRbRb+Rf
这里没有利用上MOSFET-Input-Output-Resistance中使用的负反馈公式,原因是这里的正向输入Vout到Iin的传递正向传递过程,与Iin输出再次产生的Iin是不经过同一个传函系统Rbottom的。
该电路为了保证工作,需要满足MF工作在饱和区,这就要求
Vout−VA>Vdsat⇒VA<Vout−Vdsat
这会导致VA的电压是一个比较低的存在,VA是MP的栅极电压,这导致轻载条件时,VA本身偏置得就比较小,那么MP管的潜力不会很大,限制了MP输出电流的能力。
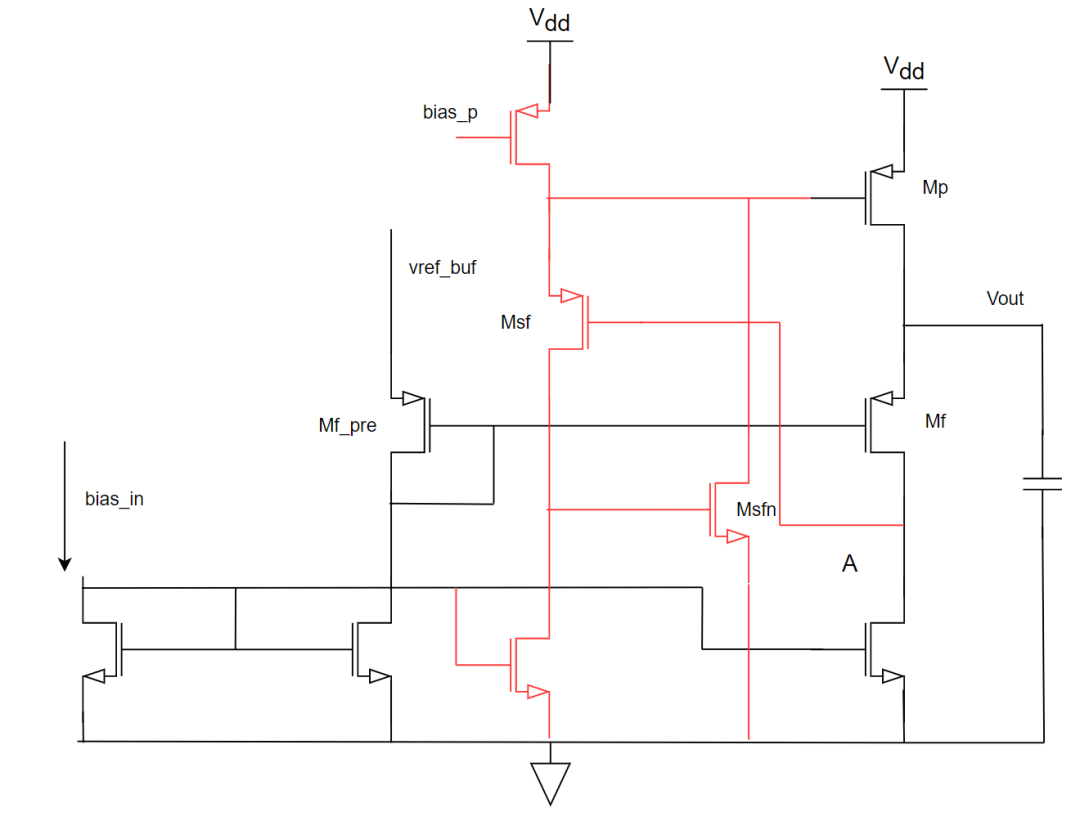
插入一级SSF(supper source follower)可以让静态工作点下的MP管的电压较高,使用较大的MP管,但是实际上MP管的电压也下不去,并没有解决MP管输出电流的能力。这里,原作者的认为SSF是为了平衡MP管栅压,我认为并非如此,这个SSF的作用,只是电位的平移,并不提供摆幅,但能提供的大电流的能力去驱动大尺寸的MP管的栅极,是为了降低内部极点,提高响应速度的。
对于以下系统,推导PSR
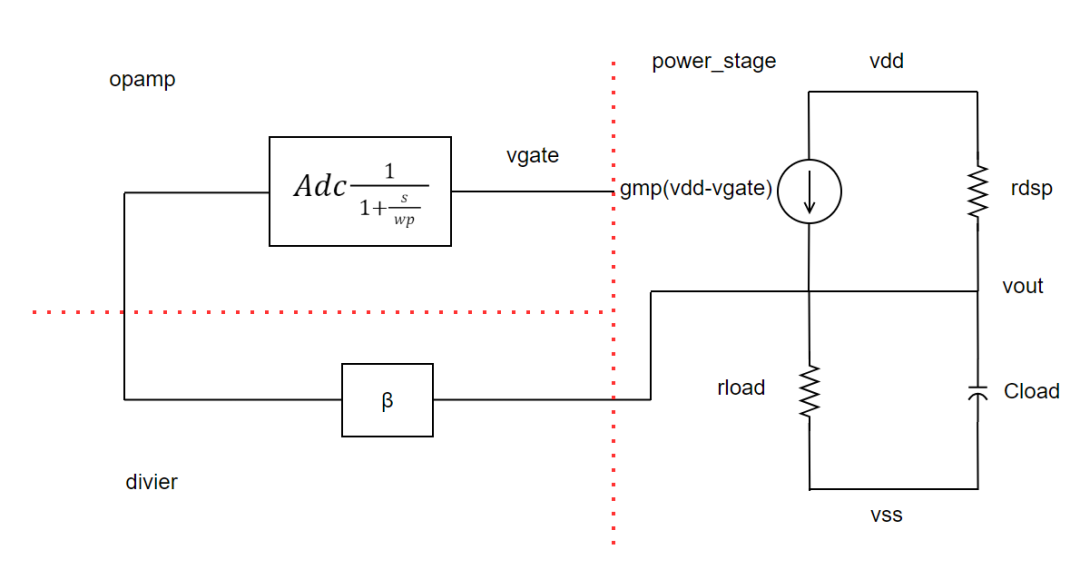
得到
PSR=VddVout=gmpβAdc+(gdsp+gload+sCload)(1+ωps)(gmp+gdsp)(1+ωps)
直观理解这个结果,上述建模分析了输出P管SOURCE注入的Vdd到输出的传递函数,这部分会被gmp放大后,负反馈后再被环路增益gmpβAdc衰减,这是DC的部分;而考虑频率响应后,衰减的能力,是受限于ωp的带宽的,此后将不再被反馈环路衰减。频率继续升高后,输出电容Cload开始提供低阻,从而实现高频下对Vdd的抑制能力;
按照以上逻辑,为了实现70dB@1MHz的PSR是非常困难的,因为这需要让运放再1MHz处仍然有70dB的增益,这意味着3.16G的GBW,这是几乎无法实现的。
GBW=1070/20×106=3.16G
所以依赖环路增益提供1MHz的PSR是不现实的。
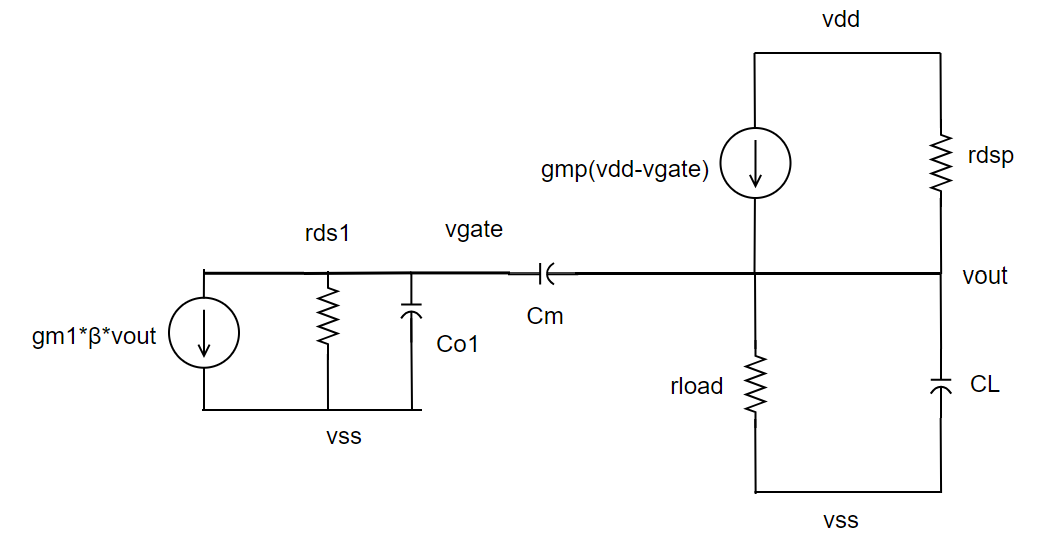
当主极点是Miller电容提供后,情况发生改变。这是因为Miller电容提供了一个快速反馈到自己Gate的一个放大器,不再需要走完完整的环路。
将输出管退化成一个Diode而不是一个源极输入的放大器。
L(nH)=0.2L×(ln(W+H2L)+0.2235(LW+H)+0.5)
这里L是导线的长度;W为导线的宽度;H为导线的厚度。



