- Cp,n,1,2,3,4表示开挂的寄生电容,彼此各不相等,用来模拟单个开关闭合时电荷左右注入的不平衡,以及开关彼此之间的失配;
- Cip,n表示对地寄生电容,某种程度也可以理解为采样电容Cs;
- Cgp,n表示运放输入端栅氧电容,主要表征输入对的Cgs以及彼此的共模;
- 没有考虑各种漏电效应,以及电容的非线性(之后会直观分析)。
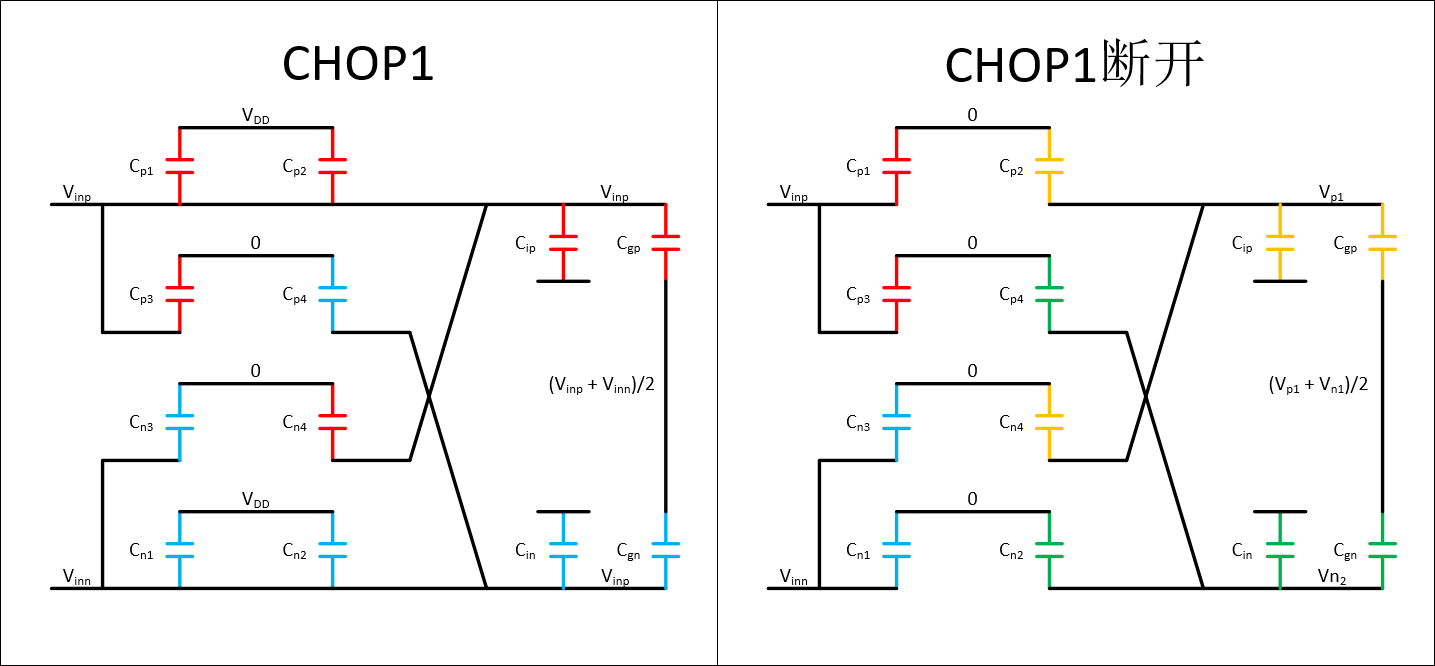
从CHOP1到CHOP1断开的阶段,计算Vinp和Vinn的电荷注入Qp1和Qn2:
⇒⎩⎪⎪⎨⎪⎪⎧(Vinp−Vdd)Cp1+Qp1=(Vinp−0)Cp1(Vinn−Vdd)Cn1+Qn1=(Vinn−0)Cn1⎩⎪⎨⎪⎧Qp1=VddCp1Qn1=VddCn1
同时需要计算Vp1,Vn1的电压,因为这会影响下一个状态:
⇒⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(Vinp−Vdd)Cp2+(Vinp−0)Cn4+(Vinp−0)Cip+(Vinp−(Vinp+Vinn/2))Cgp=(Vp1−0)Cp2+(Vp1−0)Cn4+(Vp1−0)Cip+(Vp1−(Vp1+Vp2/2))Cgp(Vinn−Vdd)Cn2+(Vinn−0)Cp4+(Vinn−0)Cin+(Vinp−(Vinn+Vinn/2))Cgn=(Vn1−0)Cn2+(Vn1−0)Cp4+(Vn1−0)Cin+(Vn1−(Vp1+Vn1/2))Cgn⎩⎪⎨⎪⎧Vp1=Vvn=
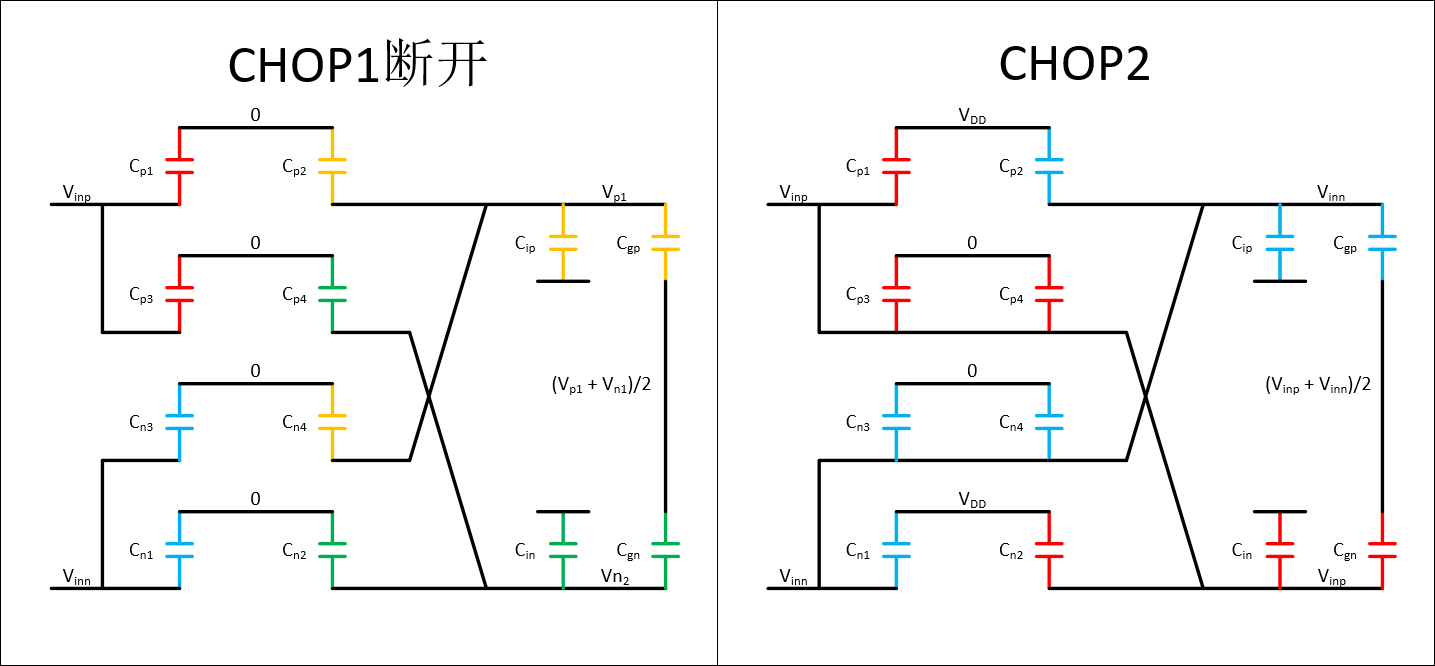
接入后,所有的电压节点都是由输入信号驱动的,计算Vinp和Vinn的电荷注入Qp2和Qn2:
⇒⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(Vinp−0)Cp1+(Vinp−0)Cp3+(Vn1−0)Cp4+(Vn1−0)Cn2+(Vn1−0)Cin+(Vn1−(Vp1+Vn1)/2)Cgn+Qp2=(Vinp−0)Cp1+(Vinp−Vdd)Cp3+(Vinp−Vdd)Cp4+(Vinp−0)Cn2+(Vinp−0)Cin+(Vinp−(Vinp+Vinn)/2)Cgn(Vinn−0)Cn1+(Vinn−0)Cn3+(Vp1−0)Cn4+(Vp1−0)Cp2+(Vp1−0)Cip+(Vp1−(Vp1+Vn1)/2)Cgn+Qn2=(Vinn−0)Cn1+(Vinn−Vdd)Cn3+(Vinn−Vdd)Cn4+(Vinn−0)Cp2+(Vinn−0)Cip+(Vinp−(Vinp+Vinn)/2)Cgn⎩⎪⎨⎪⎧Qp2=Qn2=
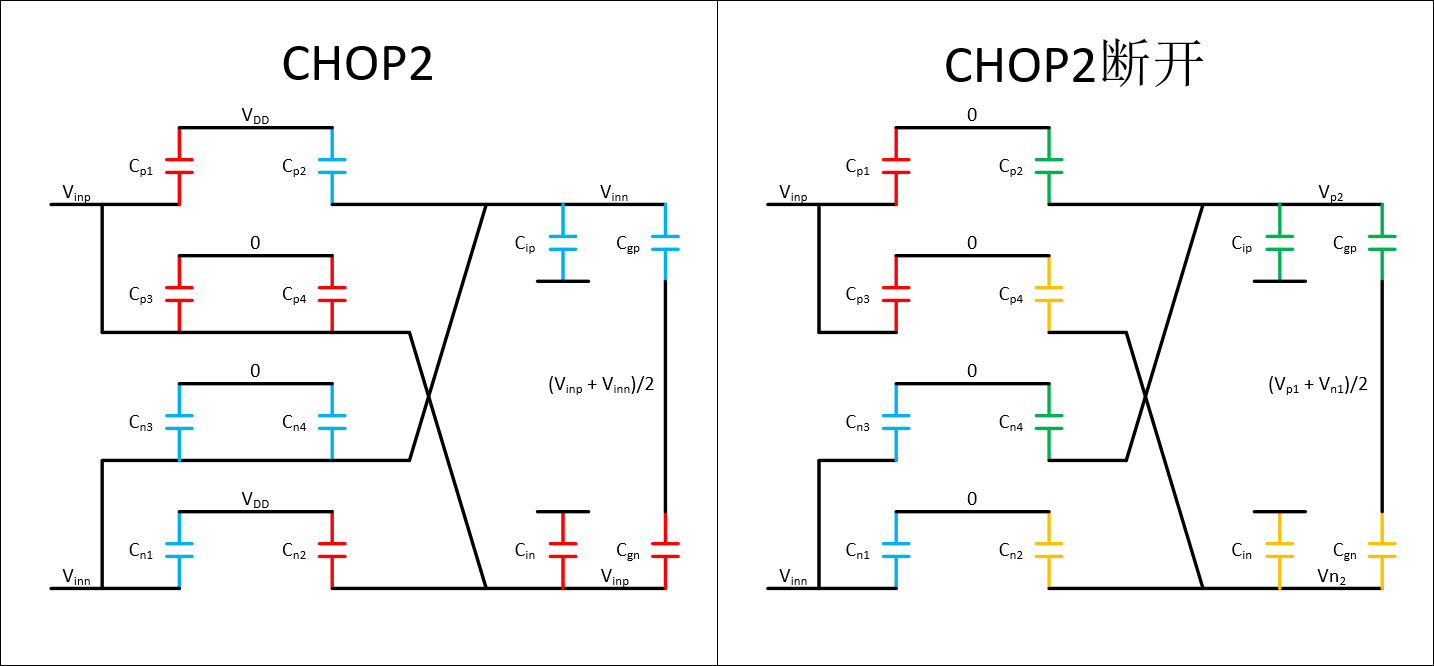
同理,从CHOP2到CHOP2断开的阶段,计算Vinp和Vinn的电荷注入Qp1和Qn2,同时计算浮空点Vp2和Vn2的电压,因为这会影响下一个状态。
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧Qp3=Qn3=Vp2=Vn2=
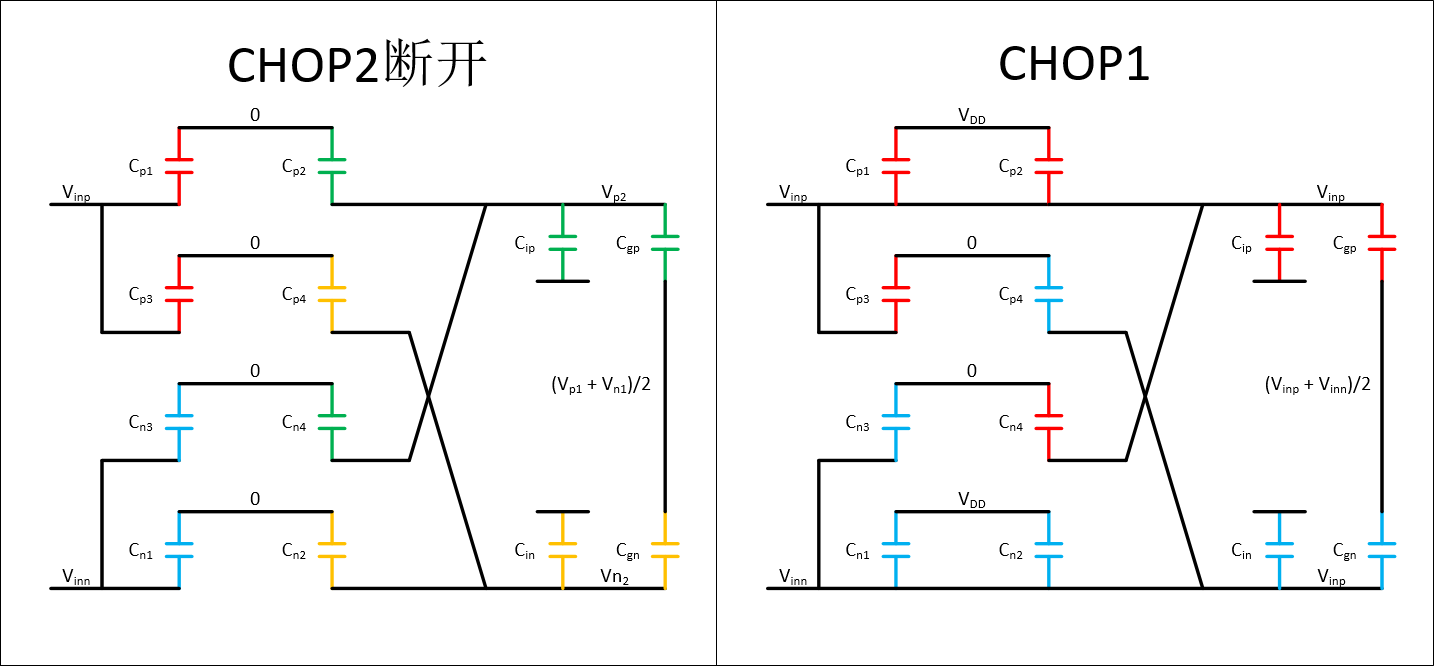
同理,从CHOP2断开到CHOP1的阶段,计算Vinp和Vinn的电荷注入Qp4和Qn4:
⎩⎪⎪⎨⎪⎪⎧Qp4=Qn4=
这个也是偏置电流的计算方法,SPEC偏置电流只计算单端。
Qp=Qp1+Qp2+Qp3+Qp4=(−Cp2−Cp4+Cn2+Cn4)Vdd+(Cp2+Cp4+Cn2+Cn4)(Vinp−Vinn)+(Cip+Cgp+Cin+Cgn)(Vinp−Vinn)
总结下来,正向输入端的输入电流:
IinputP=Qpfchop=−(ΔCswR−p1n2+ΔCswR−n1p2)Vddfchop+2(2CswR+Cparacitic+Cgg)Vdifffchop
CswR表示4个开关(SW)右手侧(Right)的平均值,Cparacitic表示正向/负向输入端对地寄生电容电容,Cgg表示正向/负向输入管的栅氧电容。
直观理解这个结果:
(1) 4个开关左手侧的电容,CswL,比如正向输入端一端总是连接着固定输入电平Vinp,另一端经历完整的Vdd→0→Vdd或者是的过程,开关注入的电荷又被吸收了回去,总体贡献为零,因此表达式中没有CswL;
(2) 分析开关右边的电容,CswR,我们就分析图示的Cp2,也就是CswR−p1,这里R表示右手侧,p1表示Positive输入端CHOP1导通的开关,激励分为电源和输入信号,利用线性叠加的原理进行分析:
- 假设输入信号为零,那么注入电荷只能由Vdd提供,CHOP1断开时从CswR−p1抽走的电荷,是CHOP导通时Vdd从CswR−n2还回去的,是否能还清,取决于−CswR−p1+CswR−n2的结果−ΔCswR−p1n2是否等于零;
- 假设输入信号不为零,而开关的导通时的电压为零,CHOP1断开时CswR−p1存储的时VinpCswR−p1的电荷,而CHOP接入时变成了VinnCswR−p1的电荷,那么这自然成为了2CVF电流,CswR−p1的作用与输入节点的寄生电容相同;
(3)输入端的对地寄生,这就是2CVF中的C,而栅极电容,input pair的正向/负向输入对的Cgs存在一个共模节点,初态时(Vinp+Vinn)/2终态仍然是,因此可以理解为一个DC节点也就是0节点,所以单端的Cgg与单端的对地寄生Cparacitic的作用是一致的。
如果将输入开关做一个bootstrap,栅极导通电压等于(Vinp+Vinn)/2+Vbst,则有
IinputP−bootstrap=−(ΔCswPR+ΔCswNR)Vbstfchop+2(2CswR+Cparacitic+Cgg)Vdifffchop
CswR表示4个开关(SW)右手侧(Right)的平均值,Cparacitic表示正向/负向输入端对地寄生电容电容,Cgg表示正向/负向输入管的栅氧电容。
似乎仅仅是将【电源电压】变成了【Bootstrap电压】,但是电容Match除了工艺的物理match,同时也要求电性上的match压差恒定,因此做bootstrap对减小【Mismatch项】有帮助。但是我们仍然观察到与输入信号相关的CVF电流。
偏置电流的计算方法,SPEC上讲absolute,应该是取绝对值的意思,因为正向输入电流为正,负向输入电流为负,为了方便计算,最终取绝对值。
Qn=Qn1+Qn2+Qn3+Qn4=(Cp2+Cp4−Cn2−Cn4)Vdd+(Cp2+Cp4+Cn2+Cn4)(Vinn−Vinp)+(Cip+Cgp+Cin+Cgn)(Vinn−Vinp)
总结下来,负向输入端的输入电流:
IinputN=Qnfchop=+(ΔCswPR+ΔCswNR)Vddfchop−2(2CswR+Cparacitic+Cgg)Vdifffchop
这个就是ADS7124上所讲的differential input current,这样得到的最终的差分电流为0
Idiff=(Qp+Qn)fchop=0
以上分析考虑到的情况是:
- 开关闭合时电荷左右的的分配不均衡;
- 开关彼此的失配,这些电容都是栅氧电容;
没有考虑到的:
- 其容值与输入电压相关,这些电容两端的压差的在不同情况下不同,那么最终的Qsum=0还成立吗?一个大胆的猜测是成立的,因为该无源二端口网络,如果平均注入电荷不为0,那么最终的电荷一定会越积越多,积累到无穷大,这显然不是事实;
- 大胆猜测,真正的原因是,这并不是一个二端口网络,电荷的注入点并非只有正/负两个端口,还有各自到VDD/GND的漏电,首先电容两个极板并非不通电荷;且栅到DIFF/BULK即使在shutdown下也有漏电电流。这些漏电与工艺相关,同时也与温度相关,因此在ADS7124的SPEC上总是会标注temperature drift。

(Qp-Qn)应该不是ADS7124上所讲的diffirentical input current,因为这个数值就是单纯的2倍的absolute input current,只会大不会小,因此不可能有单端1nA,差分400pA数据。
Qp−Qn=++=2(−Cp2−Cp4+Cn2+Cn4)Vdd2(Cp2+Cp4+Cn2+Cn4)(Vinp−Vinn)2(Cip+Cgp+Cin+Cgn)(Vinp−Vinn)2∣Qp,n∣
角标含义如下,L-p1表示Left侧开关,Postive输入端,相位1时闭合;同理,R-n2表示Right侧开关,Negtive输入端,相位2时闭合。
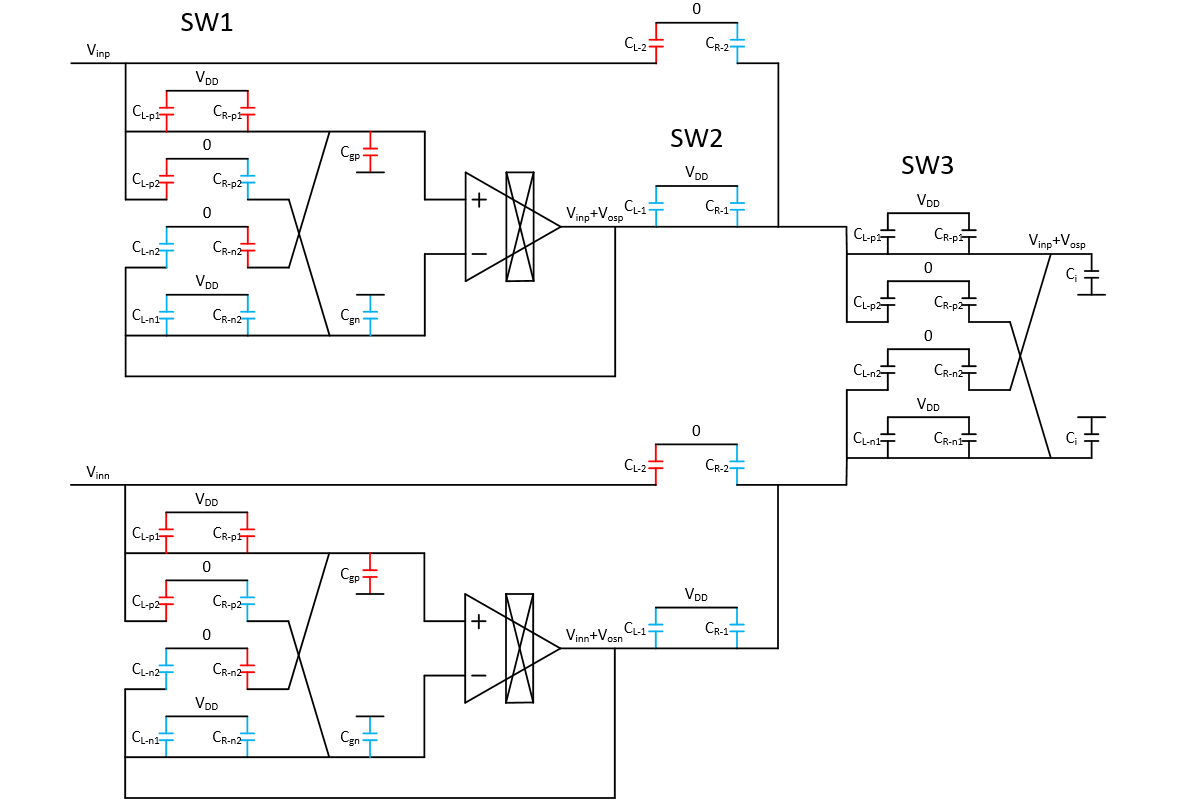
电路分为上下两个部分,只分析上半部分,正向输入端;上半部分为3部分:
- SW1,Pre-Charge Buffer的CHOP开关和输入电容,为了保证完全消除掉Vos的影响,频率应为f/2
- SW2,Pre-Charge / Fine-Settling 开关,PGA每个CHOP相位都需要完成一次Pre-Charge / Fine-Settling的动作,因此频率为2f
- SW3,PGA的CHOP开关和输入电容,CHOP频率为f
直接给出分析结论,平均输入电流将只与Buffer CHOP开关的失配电容,以及Pre-Charge / Fine-Settling的开关失配有关,与输入信号无关。如果此时将这些开关以Boostrap实现,将有助于提高电性匹配。
Ip=Qp1f1+Qp1f2+Qp3f3=−(ΔCsw1R−p1n2+ΔCsw1R−n1p2)⋅Vdd⋅2f −ΔCsw2R−12⋅Vdd⋅2f +0⋅f
这里ΔCsw1R−p1n2是Csw1R−p1−Csw1R−n2
Pre-Charge Buffer chopping开关的电荷,是从信号源来的,由于另一个输入端分别是Vinp±Vos,最终等效的输入差分电压为零,因此注入电荷之来仅来自与电源的chopping switch电荷注入,与失调无关:
Qp1=(−Csw1R−p1+Csw1R−n2)Vdd+(−Csw1R−n1+Csw1R−p2)Vdd=−(ΔCsw1R−p1n2+ΔCsw1R−n1p2)Vdd
Pre-Charge Switch和Fine-Settling开关左手侧的电容,这两个电容的一端总是接着信号源/Buffer,信号源/Buffer各自平衡各自的电荷;电容另一端,即控制信号经过Vdd→0→Vdd或者0→Vdd→0的完整周期后,平均吸走的电荷为零,因此信号源的平均注入电荷也为零;
而对于右手侧电容,Pre-Charge结束后Csw2R−1吸走的电荷,最终是需要Csw2R−2来还的,还不清的部分由信号源提供,这部分电荷取决于二者的失配:
Qp2=(−Csw2R−1+Csw2R−2)Vdd=−ΔCsw2R−12Vdd
¶ 2.2.3 SW3 Main CCIA
外部差分输入信号的CV电荷,都是由Pre-Charge Buffer提供的;栅极控制开关都是在Buffer On的情况下操作的,这部分电荷也是由Pre-Charge Buffer提供的;
Pre-Charge Buffer的失调电压,Vos,Buffer Chopping交换一次后,等效于Fine-Settling建立的电压是((Vinp+Vosp)+(Vinp−Vosp))/2=Vinp,压差为零,因此输入端注入的电荷为零。
Qp3=0
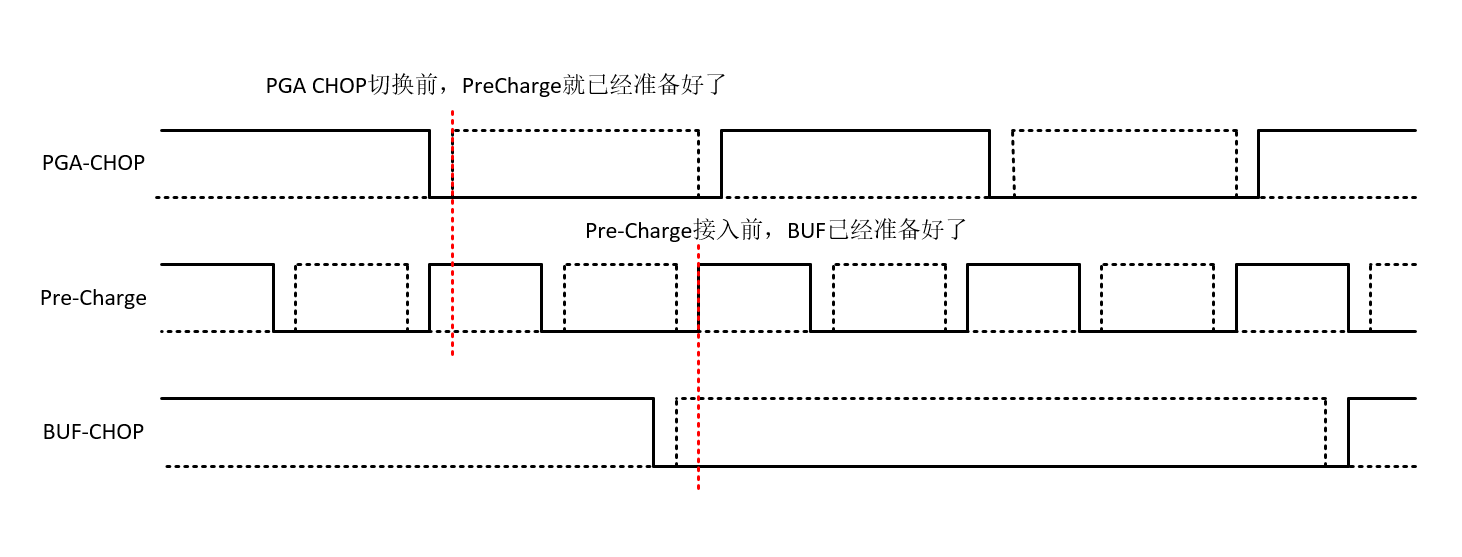
但是有一个前提:必须满足fchop−buffer≤fchop−pga/2,如果同频,则有:
(1)Buffer CHOP1,PGA CHOP1时电荷,
Qp3−1=−Vos(Csw3L−p1+Csw3L−p2+Csw3R−p1+Csw3R−n2+Cip)
(2)Buffer CHOP2,PGA CHOP2时电荷,
Qp3−2=+Vos(Csw3L−p1+Csw3L−p2+Csw3R−p2+Csw3R−n1+Cin)
(3)最终,消除掉Buffer的影响,还要依赖于这些电容的匹配
Qp3=Qp3−1+Qp3−2=−Vos(Csw3R−p1+Csw3R−n2+Cip−Csw3R−p2−Csw3R−n1−Cin)
如果Buffer的CHOP频率是PGA的一半,将经历4个过程,其中过程13抵消,24对消,最终的结果不依赖于电容的匹配
- Buffer CHOP1 - PGA CHOP1,−Vosp(Csw3R−p1+Csw3R−n2+Cip)
- Buffer CHOP1 - PGA CHOP2,−Vosp(Csw3R−p2+Csw3R−n1+Cin)
- Buffer CHOP2 - PGA CHOP1,+Vosp(Csw3R−p1+Csw3R−n2+Cip)
- Buffer CHOP2 - PGA CHOP2,+Vosp(Csw3R−p2+Csw3R−n1+Cin)
在这篇文档中,CMOS-Physics#5.2 寄生电容,概要分析了CMOS的寄生电容
NMOS从linear区切换到cut-off区,linear区沟道完全建立,器件无论从物理上,还是从电性上,source/drain本质是没有区别的。关闭的一瞬间,沟道消失,沟道上的电荷将分配到source/drain端,除了沟道电荷之外,也有gate的overlap/fringe电容上电荷的。注意,沟道在Vgs大于Vth以上会形成。
初步的结论:
- 如果Drain/Source端的负压会让沉底二极管导通,开关的电容,不去细究fringe电容的话,大约是2.5倍的W*L,通常20um/0.6um开关的电荷在36fF左右,而开关两侧的寄生电容通常足够大,通常不会出现衬底二极管导通的问题。
- Drain/Source电荷分布于其阻抗负相关:阻抗相等,电荷平均分配;阻抗越大一端,注入的电荷越少;
- 严格说阻抗是电抗,包含阻抗和容抗,X=R+tedge/(2.5C),尚不能解释为何电容的阻抗在1/(FC)基础上,又被减小了1/2.5
在初步结论上,带入数据分析:
- 开关的控制信号切换沿,在500ps左右;
- Chopping开关的左手侧一般是信号源,考虑封装PIN的寄生电容,以及外部的滤波电容,其容值大于20pF,相当于容抗为10Ω;
- 开关右手侧的电容,是采样电容,4-20pF,相当于50-10Ω@500ps,
- 输入对的寄生电容,后者小于1pF,相当于200Ω@500ps;
- 考虑512K的采样速率,信号要在1us内建立,考虑15τ的建立,那么建立switch-capacitor的RC时间常数占整个的1/3,大概在20ns,考虑到C通常在20pF左右,那么开关的阻值大约是1kΩ。
- 在BSIM4的Chapter 4和Chapter 7中,似乎对沟道电荷,栅极电荷做了详细的建模
- TSMC BCD Gen3也使用了BSIM4去给器件建模,但是TSMC使用了XPART=1的模型(0/100仿真最快,50/50最简单,40/60最符合物理实际),不是很确定这种建模机制会对仿真结果产生多大影响,暂且存疑。

(* Mathematica 13.2, Ctrl+Shift+D 分割代码,去掉";"输出结果 *)
ClearAll["Global`*"];
(* 1.1 CHOP1-CHO1断开 *)
eq11 = (vinp - vdd)*cp1 + qp1 == (vinp - 0)*cp1;
tmp = Solve[eq11, qp1];
qp1ans = tmp[[1, 1, 2]];
(* 1.2 CHOP1-CHO1断开 *)
eq12 = (vinn - vdd)*cn1 + qn1 == (vinn - 0)*cn1;
tmp = Solve[eq12, qn1];
qn1ans = tmp[[1, 1, 2]];
(* 1.3 CHOP1-CHO1断开 *)
eq13 = (vinp - vdd)*cp2 + (vinp - 0)*cn4 + (vinp - 0)*
cip + (vinp - (vinp + vinn)/2)*cgp == (vp1 - 0)*cp2 + (vp1 - 0)*
cn4 + (vp1 - 0)*cip + (vp1 - (vp1 + vn1)/2)*cgp;
(* 1.4 CHOP1-CHO1断开 *)
eq14 = (vinn - vdd)*cn2 + (vinn - 0)*cp4 + (vinn - 0)*
cin + (vinn - (vinp + vinn)/2)*cgn == (vn1 - 0)*cn2 + (vn1 - 0)*
cp4 + (vn1 - 0)*cin + (vn1 - (vp1 + vn1)/2)*cgn;
tmp = Solve[{eq13, eq14}, {vp1, vn1}];
vp1ans = tmp[[1, 1, 2]] // Expand // FullSimplify;
vn1ans = tmp[[1, 2, 2]] // ExpandAll // FullSimplify;
(* 2.1 CHOP1断开-CHO2 *)
eq21 = (vinp - 0)*cp1 + (vinp - 0)*cp3 + (vn1 - 0)*cp4 + (vn1 - 0)*
cn2 + (vn1 - 0)*cin + (vn1 - (vp1 + vn1)/2)*cgn +
qp2 == (vinp - 0)*cp1 + (vinp - vdd)*cp3 + (vinp - vdd)*
cp4 + (vinp - 0)*cn2 + (vinp - 0)*cin + (vinp - (vinp + vinn)/2)*
cgn;
tmp = Solve[eq21, qp2];
qp2ans = tmp[[1, 1, 2]] /. {vp1 -> vp1ans, vn1 -> vn1ans};
(* 2.2 CHOP1断开-CHO2 *)
eq22 = (vinn - 0)*cn1 + (vinn - 0)*cn3 + (vp1 - 0)*cn4 + (vp1 - 0)*
cp2 + (vp1 - 0)*cip + (vp1 - (vp1 + vn1)/2)*cgp +
qn2 == (vinn - 0)*cn1 + (vinn - vdd)*cn3 + (vinn - vdd)*
cn4 + (vinn - 0)*cp2 + (vinn - 0)*cip + (vinn - (vinp + vinn)/2)*
cgp;
tmp = Solve[eq22, qn2];
qn2ans = tmp[[1, 1, 2]] /. {vp1 -> vp1ans, vn1 -> vn1ans};
(* 3.1 CHOP2-CHO2断开 *)
eq31 = (vinp - vdd)*cp3 + qp3 == (vinp - 0)*cp3;
tmp = Solve[eq31, qp3];
qp3ans = tmp[[1, 1, 2]];
(* 3.2 CHOP2-CHO2断开 *)
eq32 = (vinn - vdd)*cn3 + qn3 == (vinn - 0)*cn3;
tmp = Solve[eq32, qn3];
qn3ans = tmp[[1, 1, 2]];
(* 3.3 CHOP2-CHO2断开 *)
eq33 = (vinp - vdd)*cp4 + (vinp - 0)*cn2 + (vinp - 0)*
cin + (vinp - (vinp + vinn)/2)*cgn == (vn2 - 0)*cp4 + (vn2 - 0)*
cn2 + (vn2 - 0)*cin + (vn2 - (vp2 + vn2)/2)*cgn;
(* 3.4 CHOP2-CHO2断开 *)
eq34 = (vinn - vdd)*cn4 + (vinn - 0)*cp2 + (vinn - 0)*
cip + (vinn - (vinp + vinn)/2)*cgp == (vp2 - 0)*cn4 + (vp2 - 0)*
cp2 + (vp2 - 0)*cip + (vp2 - (vp2 + vn2)/2)*cgp;
tmp = Solve[{eq33, eq34}, {vn2, vp2}];
vn2ans = tmp[[1, 1, 2]];
vp2ans = tmp[[1, 2, 2]];
(* 4.1 CHOP2断开-CHO2 *)
eq41 = (vinp - 0)*cp1 + (vinp - 0)*cp3 + (vp2 - 0)*cp2 + (vp2 - 0)*
cn4 + (vp2 - 0)*cip + (vp2 - (vp2 + vn2)/2)*cgp +
qp4 == (vinp - vdd)*cp1 + (vinp - 0)*cp3 + (vinp - vdd)*
cp2 + (vinp - 0)*cn4 + (vinp - 0)*cip + (vinp - (vinp + vinn)/2)*
cgp;
tmp = Solve[eq41, qp4];
qp4ans = tmp[[1, 1, 2]] /. {vp2 -> vp2ans, vn2 -> vn2ans};
(* 4.2 CHOP2断开-CHO2 *)
eq42 = (vinn - 0)*cn1 + (vinn - 0)*cn3 + (vn2 - 0)*cn2 + (vn2 - 0)*
cp4 + (vn2 - 0)*cin + (vn2 - (vp2 + vn2)/2)*cgn +
qn4 == (vinn - vdd)*cn1 + (vinn - 0)*cn3 + (vinn - vdd)*
cn2 + (vinn - 0)*cp4 + (vinn - 0)*cin + (vinn - (vinp + vinn)/2)*
cgn;
tmp = Solve[eq42, qn4];
qn4ans = tmp[[1, 1, 2]] /. {vp2 -> vp2ans, vn2 -> vn2ans};
(* 正向输入端 注入电荷 *)
qp = (qp1ans + qp2ans + qp3ans + qp4ans) /. {vp1 -> vp1ans,
vn1 -> vn1ans, vp2 -> vp2ans, vn2 -> vn2ans} // FullSimplify;
qpNoMismatch =
qp /. {cp1 -> csw, cp2 -> csw, cp3 -> csw, cp4 -> csw, cn1 -> csw,
cn2 -> csw, cn3 -> csw, cn4 -> csw, cip -> cp, cin -> cp,
cgp -> cgg, cgn -> cgg} // FullSimplify;
qpbst = qp /. vdd -> (vinp + vinn)/2 + vbst // FullSimplify;
qpbst /. {cp1 -> csw, cp2 -> csw, cp3 -> csw, cp4 -> csw, cn1 -> csw,
cn2 -> csw, cn3 -> csw, cn4 -> csw, cip -> cp, cin -> cp,
cgp -> cgg, cgn -> cgg, vinp -> vdiff/2, vinn -> -vdiff/2};
Collect[qpbst /. {vinp -> vdiff/2, vinn -> -vdiff/2}, vdiff] //
FullSimplify;
(* 负向输入端 注入电荷 *)
qn = (qn1ans + qn2ans + qn3ans + qn4ans) /. {vp1 -> vp1ans,
vn1 -> vn1ans, vp2 -> vp2ans, vn2 -> vn2ans} // FullSimplify;
(* 正向+负向 注入电荷 *)
sumQ = qn + qp // FullSimplify;
(* 正向-负向 注入电荷 *)
diffQ = qp - qn // FullSimplify;
diffQMismatch =
diffQ /. {cp1 -> cg, cp2 -> cg, cp3 -> cg, cp4 -> cg, cn1 -> cg,
cn2 -> cg, cn3 -> cg, cn4 -> cg} // FullSimplify;







